题目内容
16. 等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为2,则点A的坐标为(-1,$\sqrt{3}$).
等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为2,则点A的坐标为(-1,$\sqrt{3}$).
分析 过点A作AC⊥x轴于点C,然后根据三线合一即可求出AC和OC的长度.
解答 解: 过点A作AC⊥x轴于点C,
过点A作AC⊥x轴于点C,
∵∠AOB=60°
∴∠CAO=30°,
∴CO=$\frac{1}{2}$AO=1,
∴由勾股定理可知:AC=$\sqrt{3}$,
∴A(-1,$\sqrt{3}$),
故答案为(-1,$\sqrt{3}$).
点评 本题考查等边三角形的性质,解题的关键是根据等边三角形的性质求出OC与AC的长度,本题属于基础题型.

练习册系列答案
相关题目
7.下列四组有理数的大小比较正确的是( )
| A. | -$\frac{1}{3}$>-$\frac{1}{4}$ | B. | -|-1|>-|+1| | C. | $\frac{1}{3}$<$\frac{1}{4}$ | D. | |-$\frac{1}{3}$|>|-$\frac{1}{4}$| |
1.当x取什么值时,$\sqrt{9x+1}$+1取值最小,这个最小值是多少?( )
| A. | 当x=0时,最小值是2 | B. | .当x=-$\frac{1}{9}$时,最小值是1 | ||
| C. | .当x=$\frac{1}{9}$时,最小值是1 | D. | .当x=-$\frac{1}{9}$时,最小值是2 |
8.下列命题:①内错角相等;②同旁内角互补;③直角都相等;④若n<1,则n2-1<0.其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
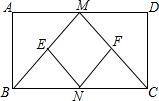 如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为20.
如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为20.