题目内容
11.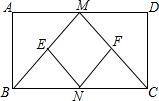 如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为20.
如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为20.
分析 根据勾股定理得出BM=CM=10,再根据E、F分别是线段BM、CM的中点,即可得出EM=FM=5,再根据N是边BC的中点,得出EM=FN,EN=FM,从而得出四边形EN,FM的周长.
解答 解:∵四边形ABCD为矩形,
∴∠A=∠D=90°,
在Rt△ABM中,AB=8,AM=6,
∴BM=$\sqrt{{6}^{2}+{8}^{2}}$=10,同法可得CM=10,
∵E、F分别是线段BM、CM的中点,BN=CN,
∴EM=FM=5,
∴EN,FN都是△BCM的中位线,
∴EN=FN=5,
∴四边形ENFM的周长为5+5+5+5=20,
故答案为20.
点评 本题考查了三角形的中位线,勾股定理以及矩形的性质,是中考常见的题型,难度不大,比较容易理解.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
2.今年参观“5•18”海交会的总人数约为489500人,将数据489500用科学记数法表示为( )
| A. | 48.95×104 | B. | 4.895×104 | C. | 4.895×105 | D. | 0.4895×106 |
19.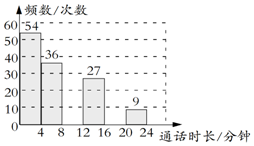 手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
(1)a的值为3;补全频数分布直方图;
(2)样本中通话时长在20<x≤24之间的9个数据分别为21分08秒,22分25秒,22分14秒,21分23秒,23分48秒,21分02秒,23分16秒,23分42秒,21分17秒,求这9个通话时长的平均数;
(3)请估计小乔家这800个通话中通话时长超过12分钟的次数.
 手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.| 通话时长x/分钟 | 次数 |
| 0<x≤4 | 54 |
| 4<x≤8 | 36 |
| 8<x≤12 | 4a |
| 12<x≤16 | 27 |
| 16<x≤20 | 4a |
| 20<x≤24 | 3a |
(2)样本中通话时长在20<x≤24之间的9个数据分别为21分08秒,22分25秒,22分14秒,21分23秒,23分48秒,21分02秒,23分16秒,23分42秒,21分17秒,求这9个通话时长的平均数;
(3)请估计小乔家这800个通话中通话时长超过12分钟的次数.
6.若方程组$\left\{\begin{array}{l}{2x+y=5}\\{x+2y=a-3}\end{array}\right.$的解满足x+y的值为非负数,则a满足( )
| A. | a<-2 | B. | a≤-2 | C. | a≤2 | D. | a≥-2 |
20.在下列现象中,属于平移的是( )
| A. | 小郭荡秋千运动 | B. | 月亮绕地球运动 | ||
| C. | 东风-5A洲际导弹击中目标后爆炸 | D. | 算盘上拨珠子 |
1.当x满足什么条件时,式子$\sqrt{3-x}$在实数范围内有意义( )
| A. | x≥0 | B. | x≥3 | C. | x≤0 | D. | x≤3 |
 等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为2,则点A的坐标为(-1,$\sqrt{3}$).
等边△ABC在平面直角坐标系内的位置如图所示,已知△ABC的边长为2,则点A的坐标为(-1,$\sqrt{3}$).


