题目内容
2.线段AB=18cm,点C是AB的黄金分割点,且AC>BC,求AC=(9$\sqrt{5}$-9)cm,BC=(27-9$\sqrt{5}$)cm.分析 由于点C是线段AB的黄金分割点(AC>BC),根据黄金分割的定义得到AC=$\frac{\sqrt{5}-1}{2}$AB,然后把AB=10cm代入计算即可.
解答 解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=$\frac{\sqrt{5}-1}{2}$AB,
∵AB=18cm,
∴AC=(9$\sqrt{5}$-9)cm,BC=AB-AC=(27-9$\sqrt{5}$)cm
故答案为:(9$\sqrt{5}$-9)cm,(27-9$\sqrt{5}$)cm.
点评 本题主要考查了黄金分割的定义:线段上一点把线段分成两段,其中较长线段是较短线段和整个线段的比例中项,即较长线段是整个线段的$\frac{\sqrt{5}-1}{2}$倍,那么这个点就是这条线段的黄金分割点,难度适中.

练习册系列答案
相关题目
13.下列实数中,是无理数的是( )
| A. | $\frac{1}{7}$ | B. | -7 | C. | 0.$\stackrel{•}{7}$ | D. | π |
17.一个直角三角形的两直角边长分别为3和4,那么它斜边上的高线长为( )
| A. | 5 | B. | 2.5 | C. | 2.4 | D. | 2 |
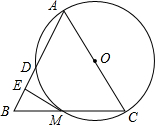 以△ABC的边AC为直径作⊙O,与AB、BC相交于点D、M,ME为⊙O的切线,ME⊥AB于E.
以△ABC的边AC为直径作⊙O,与AB、BC相交于点D、M,ME为⊙O的切线,ME⊥AB于E.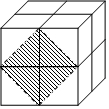 如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.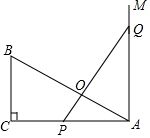 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.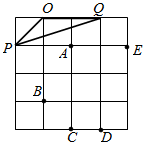 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.