题目内容
17.一个直角三角形的两直角边长分别为3和4,那么它斜边上的高线长为( )| A. | 5 | B. | 2.5 | C. | 2.4 | D. | 2 |
分析 根据勾股定理求出斜边的长,再根据面积法求出斜边上的高.
解答 解:设斜边长为c,高为h.
由勾股定理可得:c2=32+42,
则c=5,
直角三角形面积S=$\frac{1}{2}$×3×4=$\frac{1}{2}$×c×h
可得h=2.4,
故选:C.
点评 本题考查了利用勾股定理求直角三角形的边长及利用面积法求直角三角形的高,是解此类题目常用的方法.

练习册系列答案
相关题目
8.下列二次根式中,最简二次根式为( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{6}$ | C. | $\sqrt{9}$ | D. | $\sqrt{18}$ |
7.下列说法正确的是( )
| A. | 处于中间位置的数为这组数的中位数 | |
| B. | 中间两个数的平均数为这组数的中位数 | |
| C. | 想要了解一批电磁炉的使用寿命,适合采用全面调查的方法 | |
| D. | 公司员工月收入的众数是3500元,说明该公司月收入为3500元的员工最多 |
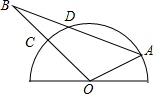 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°. 如图,已知AB=AC,DE垂直平分AB交AB、AC于D、E两点,若AB=12cm,BC=8cm,则△BCE的周长为20cm.
如图,已知AB=AC,DE垂直平分AB交AB、AC于D、E两点,若AB=12cm,BC=8cm,则△BCE的周长为20cm.