题目内容
已知关于x的方程(1-2m2)x2-4(m-1)x-4=0,求:
(1)m为何值时,两根互为倒数;
(2)m为何值时,两实数根中有一根为1.
(1)m为何值时,两根互为倒数;
(2)m为何值时,两实数根中有一根为1.
考点:根与系数的关系,一元二次方程的解
专题:
分析:(1)可设方程的一根为a,则得另一根为
,根据根与系数的关系,求出两根之和与两根之积,列出方程组,解出即可.
(2)根据根于系数的关系求得另一个根,再根据x1+x2=-
列出方程解方程即可.
| 1 |
| a |
(2)根据根于系数的关系求得另一个根,再根据x1+x2=-
| b |
| a |
解答:解:∵关于x的一元二次方程(1-2m2)x2-4(m-1)x-4=0.若方程的两根互为倒数,
设方程的一根为a,则得另一根为
,
∴
=1
1-2m2≠0
△=[-4(m-1)]2-4(1-2m2)×(-4)≥0.
解得m=±
所以m=±
时,两根互为倒数.
(2)∵关于x的一元二次方程(1-2m2)x2-4(m-1)x-4=0.两实数根中有一根为1,
∴方程的另一根为:
,
∴1+
=
,解得:m=-1±
.
所以m=-1±
时,两实数根中有一根为1.
设方程的一根为a,则得另一根为
| 1 |
| a |
∴
| -4 |
| 1-2m2 |
1-2m2≠0
△=[-4(m-1)]2-4(1-2m2)×(-4)≥0.
解得m=±
| ||
| 2 |
所以m=±
| ||
| 2 |
(2)∵关于x的一元二次方程(1-2m2)x2-4(m-1)x-4=0.两实数根中有一根为1,
∴方程的另一根为:
| 4 |
| 2m2-1 |
∴1+
| 4 |
| 2m2-1 |
| 4(m-1) |
| 1-2m2 |
| ||
| 2 |
所以m=-1±
| ||
| 2 |
点评:本题考查根与系数的关系和判别式的有关问题,仔细分析,不难解决.

练习册系列答案
相关题目
泗水县龙城中学去年对实验器材的投资为2万元,预计明年的投资为8万元.若设该校今明两年在实验器材投资上年平均增长率是x,根据题意,下面所列方程正确的是( )
| A、2(1+x)2=8 |
| B、8(1+x)2=2 |
| C、2(1-x)2=8 |
| D、2+2(1+x)+2(1+x)2=8 |
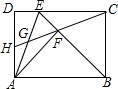 如图,在矩形ABCD,AB=
如图,在矩形ABCD,AB=