题目内容
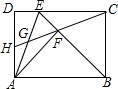 如图,在矩形ABCD,AB=
如图,在矩形ABCD,AB=| 2 |
(1)AG=FG;(2)若BC=
| 2 |
| 2 |
其中正确的个数有
考点:矩形的性质,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
专题:
分析:(1)先求得△ABF和△BCE是等腰直角三角形,得出BE=
BC,AB=
AF=
BF,结合已知得出△ABE和△FBC是等腰三角形,进而求得∠GAF=∠GFA=22.5°,即可证得AG=FG;
(2)根据已知得出AF=BF=BC=
,AB=DC=2,进而求得EF=2-
,再求得∠DCH=∠FAE=22.5°,由于∠HDC=∠EFA=90°,从而证得△HDC∽△EFA,根据相似三角形对应边成比例即可求得DH.
| 2 |
| 2 |
| 2 |
(2)根据已知得出AF=BF=BC=
| 2 |
| 2 |
解答:解:(1)在矩形ABCD中,AB=CD,AD=BC,∠ABC=90°
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠BEC=45°,
∵AF⊥BE,
∴△ABF和△BCE是等腰直角三角形,
∴BE=
BC,AB=
AF=
BF,
∵AB=
BC,
∴AF=BF=BC,AB=BE,
∴△ABE和△FBC是等腰三角形,
∴∠BAE=∠BEA=∠BFC=∠BCF=67.5°,
∴∠GAF=67.5°-45°=22.5°,∠GFA=∠FCB+∠FBC-90°=67.5°+45°-90°=22.5°,
∴∠GAF=∠GFA,
∴AG=FG,故(1)正确;
(2)∵AB=
BC,BC=
,
∴AF=BF=BC=
,AB=DC=2,
∴BE=AB=2,
∴EF=2-
,
∵∠BCF=67.5°,
∴∠DCH=90°-67.5°=22.5°,
∴∠DCH=∠FAE,
∵∠HDC=∠EFA=90°,
∴△HDC∽△EFA,
∴
=
,
即
=
,解得,DH=2
-2,故(2)正确;
故答案为:两个.
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠BEC=45°,
∵AF⊥BE,
∴△ABF和△BCE是等腰直角三角形,
∴BE=
| 2 |
| 2 |
| 2 |
∵AB=
| 2 |
∴AF=BF=BC,AB=BE,
∴△ABE和△FBC是等腰三角形,
∴∠BAE=∠BEA=∠BFC=∠BCF=67.5°,
∴∠GAF=67.5°-45°=22.5°,∠GFA=∠FCB+∠FBC-90°=67.5°+45°-90°=22.5°,
∴∠GAF=∠GFA,
∴AG=FG,故(1)正确;
(2)∵AB=
| 2 |
| 2 |
∴AF=BF=BC=
| 2 |
∴BE=AB=2,
∴EF=2-
| 2 |
∵∠BCF=67.5°,
∴∠DCH=90°-67.5°=22.5°,
∴∠DCH=∠FAE,
∵∠HDC=∠EFA=90°,
∴△HDC∽△EFA,
∴
| DH |
| EF |
| DC |
| AF |
即
| DH | ||
2-
|
| 2 | ||
|
| 2 |
故答案为:两个.
点评:本题考查了矩形的性质,等腰直角三角形的性质,等腰三角形的判定,三角形相似的判定和性质,通过角的度数相等求得角相等是本题的关键.

练习册系列答案
相关题目
1×1!+2×2!+3×3!+…+2011×2011!mod2012的值为( )(mod为取余,如27mod5=2)
| A、1 | B、3 |
| C、1006 | D、2011 |
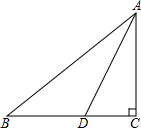 如图所示,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若AB=10,BC=8,BD=5,则△ABC的面积为
如图所示,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若AB=10,BC=8,BD=5,则△ABC的面积为 如图,△ABC被与其三边分别平行的直线分割成七个区域,如果其中的三个平行四边形与中间的三角形的面积都是1,则△ABC的面积为
如图,△ABC被与其三边分别平行的直线分割成七个区域,如果其中的三个平行四边形与中间的三角形的面积都是1,则△ABC的面积为 如图,已知扇形AOB的半径为6,∠AOB=90°,等边△CDE的顶点C、D、E分别在OA、OB、
如图,已知扇形AOB的半径为6,∠AOB=90°,等边△CDE的顶点C、D、E分别在OA、OB、