题目内容
在△ABC中,已知∠B=45°,∠C=60°,BC=5
+5,求AB和AC的长.
| 3 |
考点:解直角三角形
专题:
分析:作AD⊥BC于D,设DC=a,首先求得AD,再通过解直角三角形求得BD,从而得
a+a=5
+5,解得a=5,进而求得BD,AD,再通过解直角三角形即可求得AB和AC的长.
| 3 |
| 3 |
解答: 解:如图,作AD⊥BC于D,
解:如图,作AD⊥BC于D,
设DC=a,
在RT△ADC中,∵∠C=60°,
∴AD=tan∠C•DC=a•tan60°=
a,
在RT△ADB中,∵∠B=45°,
∴BD=AD=
a,
∴BD+DC=BC,BC=5
+5,
∴
a+a=5
+5,
解得a=5,
∴DC=5,AD=BD=5
,
∴AB=
=5
,AC=
=10.
 解:如图,作AD⊥BC于D,
解:如图,作AD⊥BC于D,设DC=a,
在RT△ADC中,∵∠C=60°,
∴AD=tan∠C•DC=a•tan60°=
| 3 |
在RT△ADB中,∵∠B=45°,
∴BD=AD=
| 3 |
∴BD+DC=BC,BC=5
| 3 |
∴
| 3 |
| 3 |
解得a=5,
∴DC=5,AD=BD=5
| 3 |
∴AB=
| AD2+BD2 |
| 6 |
| AD2+DC2 |
点评:本题主要考查正切定理在解三角形中的应用以及勾股定理的应用,考查计算能力属于基础题目.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
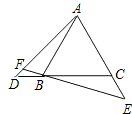 如图,点D、E分别在等边△ABC的边CB、AC为延长线上,且BD=CE,连接EB且延长交AD于F,求证:∠AFB=60°.
如图,点D、E分别在等边△ABC的边CB、AC为延长线上,且BD=CE,连接EB且延长交AD于F,求证:∠AFB=60°. 如图,△ABC中,AB=AC=5,sinB=
如图,△ABC中,AB=AC=5,sinB= 在等腰直角△ABC中,∠C=90°,M为斜边AB的中点,N为直角边AC的中点,过点C作CH⊥BN,证明:CH2=AH•MH.
在等腰直角△ABC中,∠C=90°,M为斜边AB的中点,N为直角边AC的中点,过点C作CH⊥BN,证明:CH2=AH•MH. 如图,△ABC内接于圆O,AD是⊙O的直径,经过点B作直径AD的垂线交⊙O于另一点E,交AC的延长线于点F.求证:BC•EF=AB•CF.
如图,△ABC内接于圆O,AD是⊙O的直径,经过点B作直径AD的垂线交⊙O于另一点E,交AC的延长线于点F.求证:BC•EF=AB•CF.