题目内容
19.先化简,再求值:($\frac{{x}^{2}+1}{x}$-2)÷$\frac{{x}^{2}-1}{{x}^{2}+x}$,其中x=2•sin60°+(3-π)0-$\sqrt{12}$.分析 首先对括号内的式子通分相加,把除法转化为乘法,然后计算乘法即可化简,然后化简x的值,代入数值计算即可.
解答 解:原式=$\frac{{x}^{2}+1-2x}{x}$×$\frac{x(x+1)}{(x+1)(x-1)}$
=$\frac{(x-1)^{2}}{x}$×$\frac{x(x+1)}{(x+1)(x-1)}$
=x-1,
当x=2×$\frac{\sqrt{3}}{2}$+1-2$\sqrt{3}$=-$\sqrt{3}$+1,
原式=-$\sqrt{3}$.
点评 本题考查了分式的化简求值,正确进行通分、约分是关键.

练习册系列答案
相关题目
10.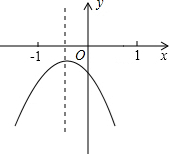 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=124度.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
14.已知a、b为实数,则a2+ab+b2-a-2b的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
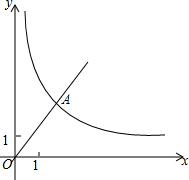 已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: