Question

10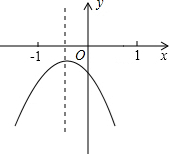．已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，在下列五个结论中，①2a-b＜0②abc＜0③a+b+c＜0④a-b+c＜0⑤4a+2b+c＞0⑤b²＞-4ac错误的个数有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，利用图象将x=1，-1，2代入函数解析式判断y的值，进而对所得结论进行判断．

解答 解：①∵由函数图象开口向下可知，a＜0，由函数的对称轴x=-$\frac{b}{2a}$＞-1，故$\frac{b}{2a}$＜1，
∵a＜0，∴b＞2a，所以2a-b＜0，①正确；

②∵a＜0，对称轴在y轴左侧，a，b同号，图象与y轴交于负半轴，则c＜0，故abc＜0；②正确；

③当x=1时，y=a+b+c＜0，③正确；

④当x=-1时，y=a-b+c＜0，④正确；

⑤当x=2时，y=4a+2b+c＜0，⑤错误；

⑥∵图象与x轴无交点，
∴△=b²-4ac＜0，
∴b²＜4ac，
∵4ac＞0
∴-4ac＜0，
∴b²＞-4ac，
∴⑥正确；
故错误的有⑤，共1个．
故选A．

点评 本题考查了图象与二次函数系数之间的关系，将x=1，-1，2代入函数解析式判断y的值是解题关键．