题目内容
11.已知抛物线y=x2+mx+7与x轴的一个交点是(3-$\sqrt{2}$,0),求m=-6,另一个交点坐标是(3+$\sqrt{2}$,0).分析 设方程x2+mx+7=0的两根分别为a、b,利用抛物线与x轴的交点问题得到a=3-$\sqrt{2}$,根据根与系数的关系得到3-$\sqrt{2}$+b=-m,(3-$\sqrt{2}$)b=7,然后先计算出b,再计算出m.
解答 解:设方程x2+mx+7=0的两根分别为a、b,则a=3-$\sqrt{2}$,
因为3-$\sqrt{2}$+b=-m,
(3-$\sqrt{2}$)b=7,
所以b=3+$\sqrt{2}$,m=-(3+$\sqrt{2}$+3-$\sqrt{2}$)=-6,
所以抛物线与x轴的另一个交点坐标为(3+$\sqrt{2}$,0).
故答案为-6,
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
相关题目
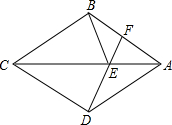 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE. 当图中各角分别满足下列条件时,你能指出哪两条直线平行?
当图中各角分别满足下列条件时,你能指出哪两条直线平行? 如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.