题目内容
7.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=124度.在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
分析 在△ABC中,∠A=62°,若点I是外接圆圆心,则根据圆周角定理可计算出∠BIC的度数;在△ABC中,O是△ABC的内心,则利用∠BOC=90°+$\frac{1}{2}$∠A求解;根据等边三角形的判定方法,当一个三角形的外心与内心恰好重合时刻判断这个三角形的现状.
解答 解:在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=2∠A=124°;
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=90°+$\frac{1}{2}$∠A=90°+25°=115°;
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
故答案为124,115°,等边三角形.
点评 本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形外心和等边三角形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在平行投影下,线段AB在投影面上的投影为线段A'B',则( )
| A. | AB=A'B' | B. | AB≥A'B' | C. | AB<A'B' | D. | 以上都有可能 |
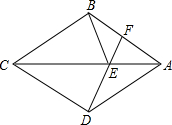 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.