题目内容
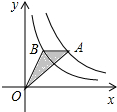 反比例函数y=
反比例函数y=| 1 |
| x |
| 2 |
| x |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
考点:反比例函数系数k的几何意义
专题:
分析:由于AB∥x轴,可知A、B两点的纵坐标相等,于是可设A点坐标是(a,c),B点坐标是(b,c),于是可得a、b的值,进而可求AB,据图可知△AOB的高是c,再利用面积公式可求其面积.
解答:解:由于AB∥x轴,设A点坐标是(a,c),B点坐标是(b,c),那么
=
,
即b=
a,
∴AB=|a-b|=
a,
∵c=
,
∴S△AOB=
AB•c=
×
a×
=
.
故选A.
| 2 |
| a |
| 1 |
| b |
即b=
| 1 |
| 2 |
∴AB=|a-b|=
| 1 |
| 2 |
∵c=
| 2 |
| a |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a |
| 1 |
| 2 |
故选A.
点评:本题考查了反比例函数系数k的几何意义,解题的关键是注意A、B两点的纵坐标相等.

练习册系列答案
相关题目
 如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )
如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )| A、点A在水中,点B在水中 |
| B、点A在水中,点B在岸上 |
| C、点A在岸上,点B在水中 |
| D、点A在岸上,点B在岸上 |
如图所示,AE的长度可表示为( )


| A、3(a-b) | B、3a-b |
| C、2a | D、2a+b |
 如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )
如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )| A、∠A=∠B |
| B、∠C=∠D |
| C、PA:PB=PC:PD |
| D、PA:PD=PC:PB |
 一位顾客在商店里挑选方台布时,他用了一种方法检验台布是否真的是正方形:拉起台布的一组对角,看是否对齐,(如图):在拉起另一组对角,看是否对齐,你认为这位顾客的检验方法正确吗?请说明理由.
一位顾客在商店里挑选方台布时,他用了一种方法检验台布是否真的是正方形:拉起台布的一组对角,看是否对齐,(如图):在拉起另一组对角,看是否对齐,你认为这位顾客的检验方法正确吗?请说明理由. 如图,直线AB,CD相交于点O,∠EOA=90°,∠COE=
如图,直线AB,CD相交于点O,∠EOA=90°,∠COE= 一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.
一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长. 如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.
如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.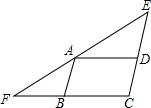 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.