题目内容
 如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )
如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )| A、∠A=∠B |
| B、∠C=∠D |
| C、PA:PB=PC:PD |
| D、PA:PD=PC:PB |
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:根据圆周角定理判断A与B;先证明△APC∽△DPB,根据相似三角形对应边的比相等即可判断C与D.
解答:解:∵⊙O中,弦AB,CD相交于P点,
∴∠A=∠D,∠C=∠B,故A与B都错误;
在△APC与△DPB中,
∵∠A=∠D,∠C=∠B,
∴△APC∽△DPB,
∴PA:PD=PC:PB,故C错误,D正确.
故选D.
∴∠A=∠D,∠C=∠B,故A与B都错误;
在△APC与△DPB中,
∵∠A=∠D,∠C=∠B,
∴△APC∽△DPB,
∴PA:PD=PC:PB,故C错误,D正确.
故选D.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了相似三角形的判定与性质.得出∠A=∠D,∠C=∠B是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
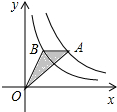 反比例函数y=
反比例函数y=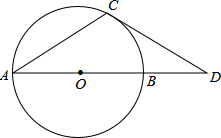 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点. 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.
如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.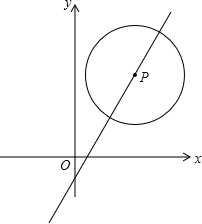 如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动. 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.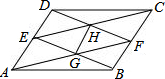 在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.
在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.