题目内容
 一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.
一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.考点:解直角三角形的应用
专题:
分析:作CD⊥AB于D.先解Rt△ACD中,求出∠ACD=30°,那么AD=
AC=4m,CD=
AD=4
m,于是DB=AB-AD=10m.然后在Rt△BCD中,由勾股定理即可求出BC的长.
| 1 |
| 2 |
| 3 |
| 3 |
解答: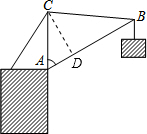 解:如图,作CD⊥AB于D.
解:如图,作CD⊥AB于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=60°,
∴∠ACD=30°,
∴AD=
AC=4m,CD=
AD=4
m,
∴DB=AB-AD=10m.
在Rt△BCD中,∵∠BDC=90°,
∴BC2=CD2+DB2=(4
)2+102=148,
∴BC=2
.
即BC的长为2
m.
 解:如图,作CD⊥AB于D.
解:如图,作CD⊥AB于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=60°,
∴∠ACD=30°,
∴AD=
| 1 |
| 2 |
| 3 |
| 3 |
∴DB=AB-AD=10m.
在Rt△BCD中,∵∠BDC=90°,
∴BC2=CD2+DB2=(4
| 3 |
∴BC=2
| 37 |
即BC的长为2
| 37 |
点评:本题考查了解直角三角形的应用,准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
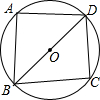 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AB=AD,若BC+CD=6,则四边形ABCD的面积为( )
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AB=AD,若BC+CD=6,则四边形ABCD的面积为( )| A、4 | B、9 | C、16 | D、25 |
下列说法不正确的是( )
| A、等腰三角形两腰上的中线相等 |
| B、等腰三角形两底角平分线相等 |
| C、等腰三角形的高,中线,角平分线互相重合 |
| D、等边三角形的高,中线,角平分线互相重合 |
 根据二次函数y=ax2+bx+c的图象草图回答下列问题:
根据二次函数y=ax2+bx+c的图象草图回答下列问题: 如图,直线AB,CD相交于点O,若∠1:∠2=1:4,则∠1=
如图,直线AB,CD相交于点O,若∠1:∠2=1:4,则∠1=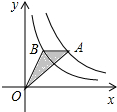 反比例函数y=
反比例函数y= 如图,?ABCD的周长是36,由钝角顶点D向AB、BC引两条角DE、DF,且DE=4,DF=6,求这个平行四边形的面积.
如图,?ABCD的周长是36,由钝角顶点D向AB、BC引两条角DE、DF,且DE=4,DF=6,求这个平行四边形的面积. 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.
如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.