题目内容
6．解下列方程（组）：（1）$\left\{\begin{array}{l}x-y=5\\ 2x+y=7\end{array}\right.$
（2）x2+6x-7=0．
分析 （1）利用加减消元法进行解答；
（2）利用“十字相乘法”对等式的左边进行因式分解．
解答 解：（1）$\left\{\begin{array}{l}{x-y=5①}\\{2x+y=7②}\end{array}\right.$，
由①+②，得3x=12，
解得x=4③
把③代入①解得y=-1．
则原方程组的解为：$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$；
（2）由原方程，得
（x-1）（x+7）=0，
则x-1=0或x+7=0，
解得x1=1，x2=-7．
点评 此题主要考查了二元一次方程组的解法，解题的关键是消元，消元的方法有两种：①加减法消元，②代入法消元．当系数成倍数关系式一般用加减法消元，系数为1时，一般用代入法消元．
练习册系列答案
相关题目
17．已知等腰三角形的底边长为10，腰长为13，则一腰上的高为（ ）
| A． | 12 | B． | $\frac{60}{13}$ | C． | $\frac{120}{13}$ | D． | $\frac{13}{5}$ |
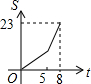
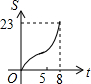
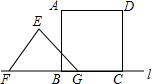如图，正方形ABCD边长为8cm，FG是等腰直角△EFG的斜边，FG=10cm，点B、F、C、G都在直线l上，△EFG以1cm/s的速度沿直线l向右做匀速运动，当t=0时，点G与B重合，记t（0≤t≤8）秒时，正方形与三角形重合部分的面积是Scm2，则S与t之间的函数关系图象大致为（ ）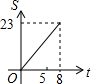
1．下列运算正确的是（ ）
| A． | -30=1 | B． | 3-2=-6 | C． | $\sqrt{9}=±3$ | D． | -32=-9 |
如图，某渔船在A处观测到灯塔M在它的北偏东48°方向上，这艘渔船以每小时28海里的速度向正东方向航行，半小时后到达B处，在B处观测到灯塔M在它的北偏东37°方向上．这艘渔船继续向正东航行多少海里，距离灯塔M最近？（参考数据：sin37°≈$\frac{3}{5}$，tan37°≈$\frac{3}{4}$，sin48°≈$\frac{7}{10}$，tan48°≈$\frac{11}{10}$，cos37°≈$\frac{4}{5}$，cos48°≈$\frac{7}{11}$）
数学老师在如图所示的黑板上写了一个关于x，y的方程，若$\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$和$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-4}\end{array}\right.$是该方程的两组解，则m，n的值分别为（ ）
如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE于G点，交DF于F点，CE交DF于H点，交BE于E点．