题目内容
16.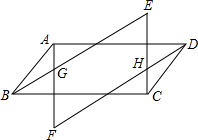 如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点,交BE于E点.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点,交BE于E点.求证:△EBC≌△FDA.
分析 由平行四边形的性质得出AD=BC,AD∥BC,由平行四边形的判定方法易证四边形BMDK和四边形AJCN是平行四边形,得出∠FAD=∠ECB,∠ADF=∠EBC,进而证明△EBC≌△FDA.
解答 证明:如图所示:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AF∥CE,BE∥DF,
∴四边形BMDK和四边形AJCN是平行四边形,
∴∠FAD=∠ECB,∠ADF=∠EBC,
在△EBC和△FDA中,$\left\{\begin{array}{l}{∠EBC=∠ADF}&{\;}\\{BC=AD}&{\;}\\{∠BCE=∠DAF}&{\;}\end{array}\right.$,
∴△EBC≌△FDA(ASA).
点评 本题考查了平行四边形的判定与性质以及全等三角形的判定;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
11. 如图,AB∥CD,∠B+∠D=80°,则∠E+∠F的度数为( )
如图,AB∥CD,∠B+∠D=80°,则∠E+∠F的度数为( )
 如图,AB∥CD,∠B+∠D=80°,则∠E+∠F的度数为( )
如图,AB∥CD,∠B+∠D=80°,则∠E+∠F的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 120° |
8.下列根式中是最简二次根式的是( )
| A. | $\sqrt{0.4}$ | B. | $\sqrt{4x}$ | C. | $\sqrt{{x^2}-4}$ | D. | $\sqrt{{m^3}-2{m^2}+m}$ |
6.某种计算机完成一次基本运算的时间约为1纳秒(μm),即0.000000001s,这个数用科学记数法表示为( )
| A. | 1×10-8s | B. | 1×10-9s | C. | 10×10-10s | D. | 0.1×10-8s |
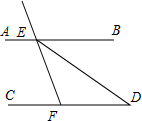 如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.