题目内容
14．
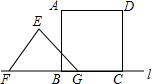如图，正方形ABCD边长为8cm，FG是等腰直角△EFG的斜边，FG=10cm，点B、F、C、G都在直线l上，△EFG以1cm/s的速度沿直线l向右做匀速运动，当t=0时，点G与B重合，记t（0≤t≤8）秒时，正方形与三角形重合部分的面积是Scm2，则S与t之间的函数关系图象大致为（ ）| A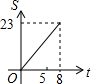． |  | B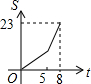． |  | C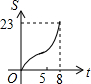． |  | D． |  |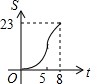
分析 根据题意可知，正方形与三角形重合部分共有两种情况，第一种是当0≤t≤5，第二种当5＜t≤8，然后分别列出S关于t的关系式即可得出答案．
解答 解：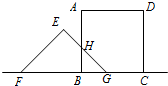
当0≤t≤5时，
设FG与AB交于点H，
∴正方形与三角形重合部分的面积是△BHG的面积，
∴BG=t，
∵∠EGF=45°，
∴BH=BG=t，
∴S=$\frac{1}{2}$BG•BH=$\frac{1}{2}$t2，
当5＜t≤8时，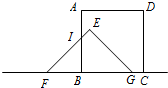
设EF与AB交于点I，
∴正方形与三角形重合部分的面积是四边形BIEG的面积，
∴BG=t，
∴FB=10-t，
∵∠EFG=45°，
∴FB=BI=10-t，
又∵△EFG的面积为：$\frac{1}{4}F{G}^{2}$=25，
∴S=25-$\frac{1}{2}$FB•BI=25-$\frac{1}{2}$（10-t）2=-$\frac{1}{2}$t2+10t-25，
故选（D）
点评 本题考查二次函数的图象，解题关键是需要根据题目条件得出两种情况下的解析式，进而根据t的取值范围去判断函数的图象．本题也涉及等腰三角形的性质，题目知识较为综合，需要学生准确进行分类讨论从而得出答案．
练习册系列答案
学业测评一课一测系列答案
相关题目
10．下列调查中，适合普查的是（ ）
| A． | 一批手机电池的使用寿命 | B． | 中国公民保护环境的意识 | ||
| C． | 你所在学校的男、女同学的人数 | D． | 端午节期间苏州市场上粽子的质量 |
5．若$\frac{{a}^{-1}+b}{a+{b}^{-1}}$=k，则$\frac{{a}^{-2}+{b}^{2}}{{a}^{2}+{b}^{-2}}$=（ ）
| A． | k | B． | $\frac{1}{2}$k | C． | k2 | D． | $\frac{1}{2}$k2 |
2．甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别从A，B两端同时出发，分别到另一端点处掉头，掉头时间不计．甲、乙两人距A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200）如图所示．综合图象信息解答下列问题：
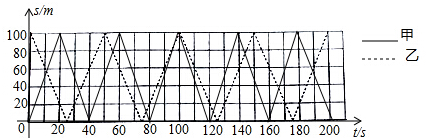
（1）求甲乙两人的速度；
（2）完成下列表格：
（3）在（2）的基础上，通过计算判断，当t=390s时，他们是否相遇？若相遇，应是第几次？并求出此时甲离A端的距离．
（1）求甲乙两人的速度；
（2）完成下列表格：
| 两人相遇次数（单位：次） | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和（单位：m） | 100 | 300 | 500 | 700 | … | 200n-100 |