Question

15．如图，已知在等边△ABC中，D为AB上一点，F为射线AC上一点，连DF交BC于点E，且DE=FE，BE=5，求AF的长．

Answer 1

分析 过点D作DM∥AC交BC于点M，可得到△DMB为等边三角形，可得到BD=BM；根据平行，易证△DEM≌△FEC，推出ME=CE，根据等边三角形及BD：DA=1：4，设未知数，表示出BM、EM的长度，进而求得AF的长度．

解答 解：如图，过点D作DM∥AC，交BC于点M，则△DMB为等边三角形，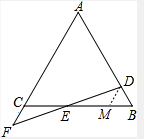
∴BD=BM；
∵DM∥AC，
∴∠F=∠EDM，
∵∠CEF=∠MED，DE=FE，
在△DEM和△FEC中，
$\left\{\begin{array}{l}{∠EDM=∠F}\\{DE=FE}\\{∠DEM=∠FEC}\end{array}\right.$，
∴△DEM≌△FEC（ASA），
∴ME=CE，CF=DM；
∵BD：AD=1：4，
故可设BD为x，则AD为4x，
∵DM∥AC，
∴BM：MC=BD：AD=1：4，
∴BM=x，ME=CE=2x，
∵BE=5，
∴BM+ME=5，即：x+2x=5，解得：x=$\frac{5}{3}$，
∴AC=BC=5x=$\frac{25}{3}$，
∴AF=AC+CF=AC+DM=$\frac{25}{3}$+$\frac{5}{3}$=10．

点评 本题主要考查全等三角形的性质和判定、等边三角形的性质和判定的综合运用，构建全等的三角形，作出正确的辅助线是解决此题的关键．