题目内容
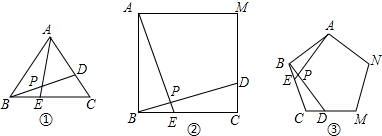
如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.图①中,∠APD的度数为60°,图②中,∠APD的度数为90°,则图③中,∠APD的度数为 .

考点:全等三角形的判定与性质
专题:常规题型
分析:图③中,根据AB=BC,BE=CD可以证明△ABE≌△BCD,可得∠EBP=∠BAE,可以求得∠APD的度数.
解答:解:正五边形各内角相等,则∠ABE=∠BCD
∵在△ABE和△BCD中,
,
∴△ABE≌△BCD,
∴∠EBP=∠BAE,
∴∠APD=∠BPE=180°-∠EBP-∠BEP
∵∠EBP=∠BAE,
∴∠APD=180°-∠BAE-∠BEP=∠ABE.
∵正五边形各内角均为108°,
∴∠APD=108°.
∵在△ABE和△BCD中,
|
∴△ABE≌△BCD,
∴∠EBP=∠BAE,
∴∠APD=∠BPE=180°-∠EBP-∠BEP
∵∠EBP=∠BAE,
∴∠APD=180°-∠BAE-∠BEP=∠ABE.
∵正五边形各内角均为108°,
∴∠APD=108°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中熟练运用SAS方法求证三角形全等是解题的关键.

练习册系列答案
相关题目
已知△ABC的内切圆⊙O切三角形的三边于点D,E,F,则△DEF是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、都有可能 |
 如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2.
如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2.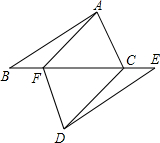 如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由.
如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由. 如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.
如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.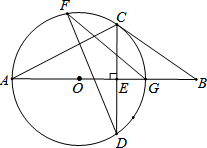 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.