题目内容
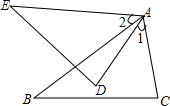已知：如图，AB=AE，∠1=∠2，AD=AC求证：BC=ED．
考点：全等三角形的判定与性质
专题：证明题
分析：根据题干中条件易证∠CAB=∠EAD，即可证明△ACB≌△ADE，可得BC=DE．
解答：证明：∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，即∠CAB=∠EAD，
在△ACB和△ADE中，
，
∴△ACB≌△ADE（SAS），
∴BC=DE．
∴∠1+∠DAC=∠2+∠DAC，即∠CAB=∠EAD，
在△ACB和△ADE中，
|
∴△ACB≌△ADE（SAS），
∴BC=DE．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证三角形全等是解题的关键．
练习册系列答案
相关题目
如图，等腰△ABC中，AB=AC=5，∠BAC=45°，以BC为直角边，以B为直角顶点向三角形外作等腰直角△BCD，则AD的长为
已知：⊙O和⊙O′交于A、B两点，过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点，GC、GD分别交⊙O和⊙O′于点E、F，求证：∠EAF=∠C+∠D．
如图，OA=OC，OD=OB，∠A=50°，∠B=30°，则∠BOC的度数为
如图，AB=CD，AD=BC，O为BD上任意一点，过O点的直线分别交AD、BC于M、N两点．求证：∠1=∠2．已知△ABC的内切圆⊙O切三角形的三边于点D，E，F，则△DEF是（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、都有可能 |
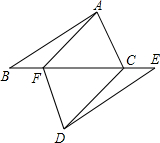如图，已知△ABF≌△DEC，且AC=DF，说明△ABC≌△DEF的理由．