题目内容
11.计算:$\sqrt{1{0}^{2}}$+4×$\root{3}{-\frac{1}{8}}$+|$\sqrt{2}$-2|.分析 先根据$\sqrt{{a}^{2}}$=|a|化简$\sqrt{1{0}^{2}}$,根据立方根的意义,计算$\root{3}{-\frac{1}{8}}$,根据绝对值的意义化简|$\sqrt{2}$-2|,再根据实数的计算法则得到最后的结果.
解答 解:原式=10+4×(-$\frac{1}{2}$)+2-$\sqrt{2}$
=10-2+2-$\sqrt{2}$
=10-$\sqrt{2}$.
点评 本题考查了二次根式的化简、立方根的求法及绝对值的化简,由于综合性较强,是中考题中常见题型.解决此类题目的关键是熟练掌握二次根式、绝对值的化简及实数的运算.

练习册系列答案
相关题目
16.某公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,2015年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
(1)若2014年底12月份奖金为a元,用代数式表示2015年二月的奖金;
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?它们相差多少元?
(3)若2015年这七个月中这名员工最多得到的奖金是2800元,请问2014年12月份他得到多少奖金?
| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 钱数变化 | +300 | +220 | -150 | -100 | +330 | +200 | +280 |
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?它们相差多少元?
(3)若2015年这七个月中这名员工最多得到的奖金是2800元,请问2014年12月份他得到多少奖金?
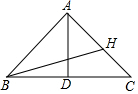 如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.
如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.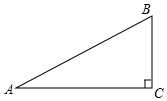 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.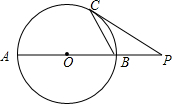 如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小.
如图,在⊙O中,AB为直径,C为⊙O上一点,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小. 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.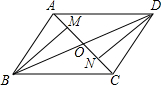 如图,?ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点,求证:BM∥DN,且BM=DN.
如图,?ABCD的对角线AC,BD相交于点O,M,N分别是OA,OC的中点,求证:BM∥DN,且BM=DN.