题目内容
19.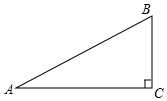 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)用尺规在AC边上求作点D,使AD=BD;(保留痕迹,不写作法)
(2)若(1)中所得BD平分∠ABC,则∠A=30°.(直接写出结果).
分析 (1)分别以点A,B为圆心,大于$\frac{1}{2}$AB长为半径画弧,交于两点,过这两点作直线交AC于点D,则点D即为所求;
(2)根据AD=BD,以及BD平分∠ABC,可得∠A=∠CBD=∠ABD,再根据三角形内角和定理,求得∠A的度数.
解答 解:(1)如图所示,点D即为所求;
(2)∵AD=BD,
∴∠A=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∵∠C=90°,
∴∠A+∠ABD+∠CBD=90°,即3∠A=90°,
∴∠A=30°.
故答案为:30°.
点评 本题主要考查了基本作图,线段垂直平分线的性质以及等腰三角形的性质的运用,解决问题的关键是掌握:等腰三角形的两个底角相等,即等边对等角.

练习册系列答案
相关题目
14.已知A、B在数轴上分别表示的数为m、n.
(1)对照数轴完成下表:
(2)若A、B两点间的距离为d,试问d与m、n有何数量关系?
(3)已知A、B在数轴上分别表示的数为x和-2,则A、B两点的距离d可表示为d=|x+2|,如果d=3,求x的值.
(4)若数轴上表示数m的点位于-5和3之间,求|m+5|+|m-3|的值.
(1)对照数轴完成下表:
| m | 5 | -3 | -4 | -4 |
| n | 2 | 0 | 3 | -2 |
| A、B两点间的距离 | 3 | 3 | 7 | 2 |
(3)已知A、B在数轴上分别表示的数为x和-2,则A、B两点的距离d可表示为d=|x+2|,如果d=3,求x的值.
(4)若数轴上表示数m的点位于-5和3之间,求|m+5|+|m-3|的值.
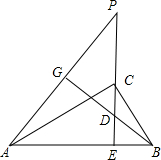 如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.
如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.