题目内容
6．
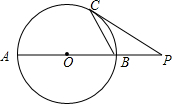如图，在⊙O中，AB为直径，C为⊙O上一点，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=27°，求∠P的大小．
分析 连接OC，如图，先利用等腰三角形的性质得到∠OCA=∠A=27°，再根据三角形外角性质得到∠POC=54°，接着根据切线的性质得到∠PCO=90°，然后利用互余计算∠P的度数．
解答 解：连接OC，如图，
∵OA=OC，
∴∠OCA=∠A=27°，
∴∠POC=∠A+∠OCA=54°，
∵PC为切线，
∴OC⊥PC，
∴∠PCO=90°，
∴∠P=90°-∠POC=90°-54°=36°．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
名校课堂系列答案
相关题目
14．已知A、B在数轴上分别表示的数为m、n．
（1）对照数轴完成下表：
（2）若A、B两点间的距离为d，试问d与m、n有何数量关系？
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
（1）对照数轴完成下表：
| m | 5 | -3 | -4 | -4 |
| n | 2 | 0 | 3 | -2 |
| A、B两点间的距离 | 3 | 3 | 7 | 2 |
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
1．
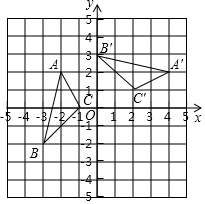如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为（ ）
如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为（ ）| A． | （0，1） | B． | （0，-1） | C． | C（1，-1） | D． | （1，0） |
18．
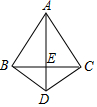如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（ ）
如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（ ）| A． | AD垂直平分BC | B． | AB=2BD | C． | ∠ACD=90° | D． | △ABD≌△ACD |
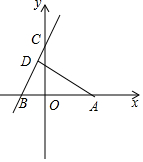如图，在直角坐标系xOy中，点A（2，0）和点B（-2，0），直线BC与y轴正半轴交于点C（0，b），过点A作AD⊥BC，垂足为D，联结OD．