题目内容
3．
如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．求证：AB=BE．
分析 连接OD，根据切线的性质得OD⊥PC，由于BE⊥PC，则可判断OD∥BE，根据平行线的性质得∠E=∠ODA，然后证明∠OAD=∠E得到BA=BE．
解答 证明：连接OD，如图，
∵PD切⊙O于点D，
∴OD⊥PC，
∵BE⊥PC，
∴OD∥BE，
∴∠E=∠ODA，
∵OA=OD，
∴∠ODA=∠OAD，
∴∠OAD=∠E，
∴BA=BE．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
相关题目
13．下列汽车标志中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
14．已知A、B在数轴上分别表示的数为m、n．
（1）对照数轴完成下表：
（2）若A、B两点间的距离为d，试问d与m、n有何数量关系？
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
（1）对照数轴完成下表：
| m | 5 | -3 | -4 | -4 |
| n | 2 | 0 | 3 | -2 |
| A、B两点间的距离 | 3 | 3 | 7 | 2 |
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
18．
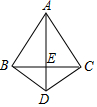如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（ ）
如图，在△ABC中，AB=AC，∠ABC=60°，D是三角形外一点，且BD=CD，AD与BC交于一点E，∠BDC=120°，则下列结论错误的是（ ）| A． | AD垂直平分BC | B． | AB=2BD | C． | ∠ACD=90° | D． | △ABD≌△ACD |
甲、乙两人从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（时）之间的关系的图象如图所示．根据图中提供的信息，有下列说法：