题目内容
16.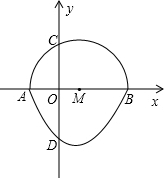 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
分析 根据圆心坐标及点C的坐标,可求出半径的长度,然后结合图形,可得点A坐标为(-1,0),点B坐标为(3,0),利用待定系数法确定抛物线解析式,因为经过点D的“蛋圆”切线过D点,所以本题可设它的解析式为y=kx-3,因为相切,所以它们的交点只有一个,进而可根据一元二次方程的有关知识解决问题.
解答 解:∵AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$),
∴半径CM=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴A(-1,0),B(3,0),
∵抛物线过点A、B,
∴设抛物线的解析式为y=a(x+1)(x-3),
又∵抛物线过点D(0,-3),
∴-3=a•1•(-3),即a=1,
∴y=x2-2x-3,
∵经过点D的“蛋圆”切线过D(0,-3)点,
∴设它的解析式为y=kx-3,
又∵抛物线y=x2-2x-3与直线y=kx-3相切,
∴x2-2x-3=kx-3,即x2-(2+k)x=0只有一个解,
∴△=(2+k)2-4×0=0,
解得:k=-2,
即经过点D的“蛋圆”切线的解析式为y=-2x-3.
故答案为:y=-2x-3.
点评 本题考查了二次函数的综合应用,需灵活运用待定系数法建立函数解析式,并利用切线的性质,结合一元二次方程来解决问题,难度一般.

练习册系列答案
相关题目
1. 我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
 我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )| A. | 48 | B. | 52 | C. | 336 | D. | 364 |
8.在Rt△ABC中,∠C=90゜,AC=3,BC=4,以C为圆心,2为半径的⊙C与AB的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
6.在下列条件中不能判定△ABC∽△DEF的是( )
| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |