题目内容
8.在Rt△ABC中,∠C=90゜,AC=3,BC=4,以C为圆心,2为半径的⊙C与AB的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
分析 根据题意可求得直角三角形斜边上的高,再根据直线和圆的位置关系,判断圆心到直线AB的距离与2的大小关系,从而确定⊙C与AB的位置关系.
解答 解:由勾股定理得AB=5,再根据三角形的面积公式得,3×4=5×斜边上的高,
∴斜边上的高=$\frac{12}{5}$,
∵$\frac{12}{5}$>2,
∴⊙C与AB相离.
故选:A.
点评 本题考查了直线和园的位置关系,解决的根据是直线和圆相离?圆心到直线的距离大于圆的半径.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
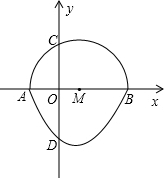 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
 如图,在△ABC中,BC=8,∠ABC和∠ACB的角平分线相交于F,FD∥AB交BC于点D,FE∥AC交BC于点E,求△DEF的周长.
如图,在△ABC中,BC=8,∠ABC和∠ACB的角平分线相交于F,FD∥AB交BC于点D,FE∥AC交BC于点E,求△DEF的周长.