题目内容
6.在下列条件中不能判定△ABC∽△DEF的是( )| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |
分析 由两角分别相等的两个三角形相似得出A能判定△ABC∽△DEF;
两边成比例,但是夹角不相等,得出B不能判定△ABC∽△DEF;
由直角三角形相似的判定方法得出C能判定△ABC∽△DEF;
由三边成比例的两个三角形相似得出D能判定△ABC∽△DEF;即可得出结论.
解答 解:A能判定△ABC∽△DEF;理由:
∵∠C=180°-∠A-∠B=180°-60°-80°=40°,
∴∠C=∠D,
又∵∠B=∠E=80°,
∴△ABC∽△FED;
B不能判定△ABC∽△DEF;理由:
∵AB:AC=DF:EF,∠A=∠D,而不是∠A=∠F,
∴不能判定△ABC∽△DEF;
C能判定△ABC∽△DEF;理由:
∵∠B=∠E=90°,
∴AC、DF分别为斜边,
∵BC:EF=AC:DF,
∴△ABC∽△DEF;
D能判定△ABC∽△DEF;理由:
∵$\frac{AB}{EF}=\frac{1}{4}$,$\frac{BC}{FD}=\frac{2}{8}=\frac{1}{4}$,$\frac{CA}{DE}=\frac{1.5}{6}=\frac{1}{4}$,
∴$\frac{AB}{EF}=\frac{BC}{FD}=\frac{CA}{DE}$,
∴△ABC∽△EFD.
故选:B.
点评 本题考查了相似三角形的判定方法、三角形内角和定理;熟练掌握相似三角形的判定方法,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
16.若分式$\frac{x-1}{(x-2)(x-3)}$=$\frac{a}{x-3}$+$\frac{b}{x-2}$(a、b为常数),则a、b的值为( )
| A. | a=4,b=-3 | B. | a=2,b=-1 | C. | a=-1,b=1 | D. | a=-1,b=2 |
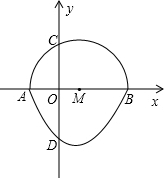 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3. 如图,在△ABC中,BC=8,∠ABC和∠ACB的角平分线相交于F,FD∥AB交BC于点D,FE∥AC交BC于点E,求△DEF的周长.
如图,在△ABC中,BC=8,∠ABC和∠ACB的角平分线相交于F,FD∥AB交BC于点D,FE∥AC交BC于点E,求△DEF的周长.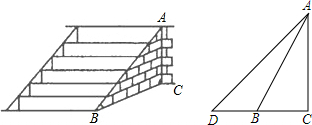
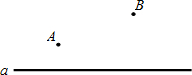 如图,直线a表示一条公路,点A、B表示两个乡镇.如果要在公路旁(直线a上)修一个车站S,使得AS+BS最小,请作出点S.
如图,直线a表示一条公路,点A、B表示两个乡镇.如果要在公路旁(直线a上)修一个车站S,使得AS+BS最小,请作出点S. 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.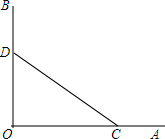 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.