题目内容
14.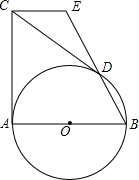 已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.
已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.
分析 根据切线的性质可得OA⊥AC,OD⊥CD,进一步得出∠AOC=∠PBD,证得四边形CEBO是平行四边形,得到CE=OB=$\frac{1}{2}$AB=1;根据勾股定理求得BE,然后根据射影定理求得BD,即可求得DE,从而求得DE:BD=3:2;由②可知:h1:h2=3:5,求得h1的值,根据面积公式求得S△CDE=$\frac{3}{5}$;解直角三角形即可求得sin∠ECD=$\frac{{h}_{1}}{CD}$=$\frac{3}{5}$;继而得到结论①②③成立.
解答 解:①连接OD,OC,
∵CA、CD是圆O的切线,
∴OA⊥AC,OD⊥CD,
∵OA=OD=1,
∴∠ACO=∠DCO,
∴∠AOC=∠DOC=$\frac{1}{2}$∠AOD,
∵∠OBD=$\frac{1}{2}$∠AOD,
∴∠AOC=∠PBD,
∴CO∥BE,
∵CE∥AB,
∴四边形CEBO是平行四边形,
∴CE=OB=$\frac{1}{2}$AB=1;
②连接OE,过O点作OF⊥BD,
∴BF=$\frac{1}{2}$BD,
∵∠EOB=90°,OE=AC=2,
∴BE=$\sqrt{O{E}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵OB2=BF•BE,
即12=$\frac{1}{2}$BD×$\sqrt{5}$,
∴BD=$\frac{2\sqrt{5}}{5}$,
∴DE=BE-BD=$\frac{3\sqrt{5}}{5}$,
∴DE:BD=3:2;
③设D到CE的距离为h1,B到CE的距离为h2,则S△CDE=$\frac{CE•{h}_{1}}{2}$,
由②可知:h1:h2=3:5,
∴h1=2×$\frac{3}{5}$=$\frac{6}{5}$,
∴S△CDE=$\frac{CE•{h}_{1}}{2}$=1×$\frac{6}{5}$×$\frac{1}{2}$=$\frac{3}{5}$;
④sin∠ECD=$\frac{{h}_{1}}{CD}$=$\frac{\frac{6}{5}}{2}$=$\frac{3}{5}$;
所以正确的结论是①②③,
故答案为①②③.
点评 本题考查了切线的性质,角平分线的判定,平行四边形的判定和性质三角形的面积以及解直角三角形等,在本题中借用切线的性质,求得相应角的关系是解题的关键.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案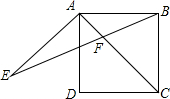 如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.
如图,在正方形ABCD中,AE=AD,∠DAE=60°,BE交AC于点F.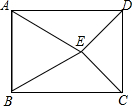 如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.
如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.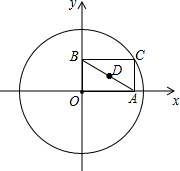 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是B的中点,如果点C在圆上运动一周,那么点D运动过的路程长为2π.
如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是B的中点,如果点C在圆上运动一周,那么点D运动过的路程长为2π.