题目内容
6.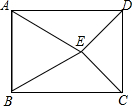 如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.
如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.
分析 由矩形和等边三角形的性质得出AD=BC,AE=BE,∠AEB=60°,由SSS证明△ADE≌△BCE,得出∠AED=∠BEC,再由四边形内角和定理即可得出结果.
解答 解:∵四边形ABCD是矩形,△ABE是等边三角形,
∴AD=BC,AE=BE,∠AEB=60°,
在△ADE和△BCE中,
$\left\{\begin{array}{l}{AD=BC}&{\;}\\{AE=BE}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△BCE(SSS),
∴∠AED=∠BEC,
∵∠DEC=90°,
∴∠AED=(360°-90°-60°)÷2=105°.
点评 本题考查了矩形的性质、等边三角形的性质、全等三角形的判定与性质、四边形内角和定理;熟练掌握矩形和等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
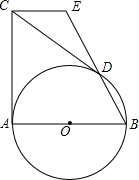 已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.
已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.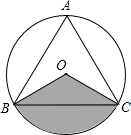 如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.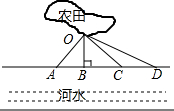 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )
春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )