题目内容
9.一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴的交点坐标为(-$\frac{b}{k}$,0),与y轴的交点坐标为(0,b).分析 分别令y=0和x=0,可求得与x轴和y轴的交点坐标.
解答 解:令y=0,可得x=-$\frac{b}{k}$,所以一次函数y=kx+b(k,b≠0)的图象与x轴的交点坐标是(-$\frac{b}{k}$,0),
令x=0,可得y=b,所以一次函数y=kx+b(k,b≠0)的图象与y轴的交点坐标是(0,b),
故答案为:-$\frac{b}{k}$,b.
点评 本题主要考查一交函数与坐标轴的交点,把交点问题转化成求方程的解的问题是这类问题的一般方法.

练习册系列答案
相关题目
17.已知$\sqrt{a+2}$+|b-1|=0,那么(a+b)2014的平方根为( )
| A. | 0 | B. | -1 | C. | 1 | D. | ±1 |
14.抛物线$y=-\frac{1}{2}{x^2}$不具有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 函数有最小值 |
1.到三角形三边距离相等的点是( )
| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三条角平分线的交点 | D. | 不能确定 |
 如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹)
如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹) 尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积.
尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积.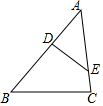 如图,在△ABC的边AB、AC上有点D、E.若∠BDE+∠C=180°,求证:$\frac{AD}{AC}$=$\frac{AE}{AB}$.
如图,在△ABC的边AB、AC上有点D、E.若∠BDE+∠C=180°,求证:$\frac{AD}{AC}$=$\frac{AE}{AB}$.