题目内容

14．抛物线$y=-\frac{1}{2}{x^2}$不具有的性质是（　　）
A．开口向下B．对称轴是y轴
C．当x＞0时，y随x的增大而减小D．函数有最小值

分析 根据二次函数的性质对各选项进行逐一分析即可．

解答 解：A、∵a=-$\frac{1}{2}$＜0，∴此函数的图象开口向下，故本选项正确；
B、∵抛物线y=-$\frac{1}{2}$x2不的顶点在原点，∴对称轴是y轴，故本选项正确；
C、当x＞0时，抛物线在第四象限，y随x的增大而减小，故本选项正确；
D、∵此函数的图象开口向下，∴函数有最大值，故本选项错误．
故选D．

点评 本题考查的是二次函数的性质，熟知二次函数y=ax2（a≠0）的性质是解答此题的关键．

练习册系列答案
相关题目
4．如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=112°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
（1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，问：直线ON是否平分∠AOC？请说明理由；
（2）将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为多少？
（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究：∠AOM与∠NOC之间的数量关系，并说明理由．
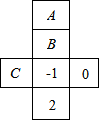5．如图是一个正方体盒子的展开图，在其中三个正方形A、B、C内分别添入适当的数，使他们折成正方体后相对的面上的两个数互为相反数，则添入正方形A、B、C内的三个数中最小的是B面．
2．计算：
（1）（-3）+（-4）-（+11）-（-19）
（2）-10-8÷（-2）×（-$\frac{1}{2}$）
（3）（$\frac{2}{3}$-$\frac{1}{2}$）×30÷（-$\frac{1}{5}$）
（4）（-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$）×|-12|
（5）18×$\frac{2}{3}$+13×$\frac{2}{3}$-4×$\frac{2}{3}$．                   
（6）（-36$\frac{9}{11}$）÷9．
9．一次函数y=kx+b（k，b为常数，且k≠0）的图象与x轴的交点坐标为（-$\frac{b}{k}$，0），与y轴的交点坐标为（0，b）．
19．计算题：
（1）（-0.9）+（+4.4）+（-8.1）+（+5.6）
（2）-3$\frac{1}{2}$×（-$\frac{6}{7}$）-（-10）÷（-$\frac{2}{3}$）
（3）-1-48×（$\frac{5}{24}$-$\frac{3}{16}$+$\frac{1}{6}$）                 
（4）-32-[（-3）2×（-$\frac{4}{3}$）-（-2）3]．
6．下列图案中，可以利用平移来设计的图案是（　　）
A．B．C．D．
3．（1）计算：$\sqrt{8}$×sin45°-（$\frac{1}{2}$）-2+|-3|
（2）化简，求值：（$\frac{1}{x+2}$+1）÷$\frac{{x}^{2}-9}{{x}^{2}+4x+4}$，其中x=4．
4．如图，在⊙O中，AB是⊙O的弦，AB=10，OC⊥AB，垂足为点D，则AD=5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网