题目内容
20.化简下列各式:(1)(2a-1)(1+2a)-(a-2)(a+3)-(a-1)2;
(2)$\frac{x-1}{{x}^{2}-9}$÷($\frac{x}{x-3}$-$\frac{5x-1}{{x}^{2}-9}$)-$\frac{1}{x+1}$.
分析 (1)根据平方差公式、多项式乘多项式及完全平方公式展开,再去括号、合并同类项即可得;
(2)先将分子分母因式分解,再依次计算括号内的和除法、减法即可.
解答 解:(1)原式=(2a)2-1-(a2+3a-2a-6)-(a2-2a+1)
=4a2-1-a2-3a+2a+6-a2+2a-1
=2a2+a+4;
(2)原式=$\frac{x-1}{(x+3)(x-3)}$÷$\frac{{x}^{2}+3x-5x+1}{(x+3)(x-3)}$-$\frac{1}{x+1}$
=$\frac{x-1}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{(x-1)^{2}}$-$\frac{1}{x+1}$
=$\frac{1}{x-1}$-$\frac{1}{x+1}$
=$\frac{x+1}{(x+1)(x-1)}$-$\frac{x-1}{(x+1)(x-1)}$
=$\frac{2}{(x+1)(x-1)}$
=$\frac{2}{{x}^{2}-1}$.
点评 本题主要考查整式的混合运算和分式的混合运算,熟练掌握整式的混合运算和分式的混合运算的顺序和法则是解题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.设a、b互为相反数,c、d互为倒数,则2013(a+b)-cd的值是( )
| A. | 2013 | B. | 0 | C. | -1 | D. | 1 |
11.下列说法:
①一个无理数的相反数一定是无理数;
②一切实数都可以进行开立方运算,只有非负数才能进行开平方运算;
③一个有理数与一个无理数的和或差一定是无理数;
④实数m的倒数是$\frac{1}{m}$.
其中,正确的说法有( )
①一个无理数的相反数一定是无理数;
②一切实数都可以进行开立方运算,只有非负数才能进行开平方运算;
③一个有理数与一个无理数的和或差一定是无理数;
④实数m的倒数是$\frac{1}{m}$.
其中,正确的说法有( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
8.过⊙O内一点M的最长的弦长为6厘米,最短的弦长为4厘米,则OM的长为( )
| A. | $\sqrt{3}$厘米 | B. | $\sqrt{5}$厘米 | C. | 2厘米 | D. | 5厘米 |
5.△ABC∽△DEF,且相似比为2:1,△ABC的面积为8,则△DEF的面积为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
 如图,在宽为24米,长为32米的矩形地面上修建三条同样宽的道路,余下部分作为耕地,若耕地面积需要690m2,则修建的路宽应为多少米?
如图,在宽为24米,长为32米的矩形地面上修建三条同样宽的道路,余下部分作为耕地,若耕地面积需要690m2,则修建的路宽应为多少米?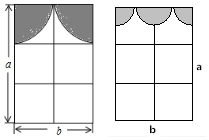 如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).