题目内容
12.阅读理解:用“十字相乘法”分解因式2x2-x-3的方法.(1)二次项系数2=1×2;
(2)常数项-3=-1×3=1×(-3),验算:“交叉相乘之和”;
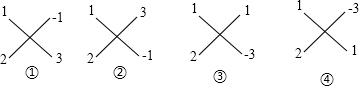
1×3+2×(-1)=1 1×(-1)+2×3=5 1×(-3)+2×1=-1 1×1+2×(-3)=-5
(3)发现第③个“交叉相乘之和”的结果1×(-3)+2×1=-1,等于一次项系数-1.
即:(x+1)(2x-3)=2x2-3x+2x-3=2x2-x-3,则2x2-x-3=(x+1)(2x-3).
像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫做十字相乘法.仿照以上方法,分解因式:3x2+5x-12=(x+3)(3x-4).
分析 根据“十字相乘法”分解因式得出3x2+5x-12=(x+3)(3x-4)即可.
解答 解:3x2+5x-12=(x+3)(3x-4).
故答案为:(x+3)(3x-4)
点评 本题考查了因式分解-十字相乘法等,解此题的关键是熟练掌握“十字相乘法”分解因式,题目比较好,难度也不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为$\frac{1}{3}$,则随机摸出一个红球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
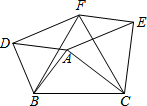 如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.
如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.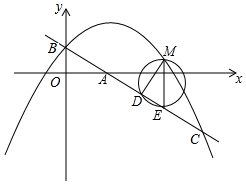 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).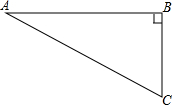 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是$\frac{\sqrt{3}}{6}$.