题目内容
2.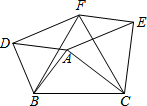 如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.
如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.
分析 根据题中的等式关系可推出两组对边分别相等,从而可判断四边形AEFD为平行四边形.由勾股定理的逆定理判定∠BAC=90°,则∠DAE=150°,故易求∠FDA=30°.所以由平行四边形的面积公式即可解答.
解答 解:∵在△ABC中,AB=5,AC=12,BC=13,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBF=∠ABC}\\{BF=BC}\end{array}\right.$
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=12,
同理可证△ABC≌△EFC,
∴AB=EF=AD=5,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°-∠DAE=30°,
∴S?AEFD=AD•(DF•sin30°)=5×(12×$\frac{1}{2}$)=30,
即四边形AEFD的面积是30,
故答案为:30.
点评 本题综合考查了勾股定理的逆定理,平行四边形的判定与性质,全等三角形的判定与性质以及等边三角形的性质.综合性比较强,难度较大,有利于培养学生综合运用知识进行推理和计算的能力.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
17.9的立方根是( )
| A. | 3 | B. | ±3 | C. | $\root{3}{9}$ | D. | $±\root{3}{9}$ |
14.等腰三角形一腰上的高与另一腰的夹角为20°,则这个等腰三角形的底角度数是( )
| A. | 70° | B. | 55° | C. | 35° | D. | 55°或35° |
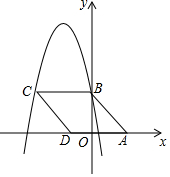 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为20.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为20.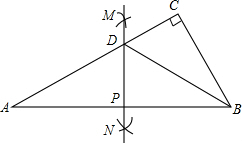 如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.
如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.