��Ŀ����
3��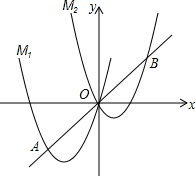 ��ͼ����������M1��y=ax2+4x����ƽ��3����λ��������ƽ��3����λ���õ�������M2��ֱ��y=x��M1��һ�������ΪA����M2��һ�������ΪB����A�ĺ�������-3��
��ͼ����������M1��y=ax2+4x����ƽ��3����λ��������ƽ��3����λ���õ�������M2��ֱ��y=x��M1��һ�������ΪA����M2��һ�������ΪB����A�ĺ�������-3����1����a��ֵ��M2�ı���ʽ��
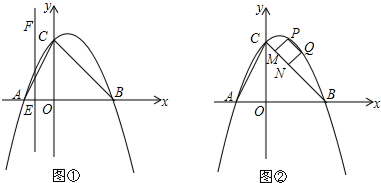
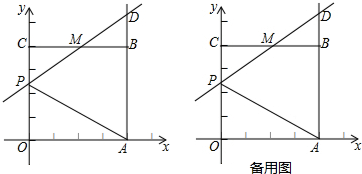
��2����C���߶�AB�ϵ�һ�����㣬����C��x��Ĵ��ߣ�����ΪD����CD���Ҳ���������CDEF��
�ٵ���C�ĺ�����Ϊ2ʱ��ֱ��y=x+nǡ�þ���������CDEF�Ķ���F�����ʱn��ֵ��
���ڵ�C���˶������У���ֱ��y=x+n��������CDEFʼ��û�й����㣬��n��ȡֵ��Χ��ֱ��д���������
���� ��1������A���������y=x�����ɵó���A�����꣬�Ӷ��ó���A�����꣬���ݵ�A��������M1��y=ax2+4x�ϣ����뼴�ɵó�a��ֵ����������M1��Ϊ����ʽ������ƽ�Ƶ�ԭ�ɵó�������M2��
��2���ٰѵ�C���������y=x�����ɵó���C���꣬�Ӷ��ó���F���꣬�ѵ�F����y=x+n���ɵó�n��ֵ��
�ڸ���ֱ��y=x+n��������CDEFʼ��û�й����㣬ֱ�ӿɵó�n��ȡֵ��Χ��
���  �⣺��1���ߵ�A��ֱ��y=x���ҵ�A�ĺ�������-3��
�⣺��1���ߵ�A��ֱ��y=x���ҵ�A�ĺ�������-3��
��A��-3��-3����
��A��-3��-3������y=ax2+4x��
���a=1��
��M1��y=x2+4x��������-2��-4����
��M2�Ķ���Ϊ��1��-1����
��M2�ı���ʽΪy=x2-2x��
��2���������⣬C��2��2����
��F��4��2����
��ֱ��y=x+n������F��
��2=4+n��
���n=-2��
��������ã�n��ȡֵ��Χ��n��3��n��-6��
���� ���⿼���˶��κ����ۺ��⣬�漰��֪ʶ�㣺�ô���ϵ������������ʽ�������ε������Լ�����ͼ���ƽ�ƣ������ϼ��¼�������Ҽ��ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
�����Ŀ
14����֪�߳�Ϊa�������ε����Ϊ8��������˵���У�������ǣ�������
| A�� | a�������� | B�� | a�Ƿ���x2-8=0�Ľ� | ||
| C�� | a��8������ƽ���� | D�� | a���㲻��ʽ$\frac{2x-4}{3}��1$ |
12��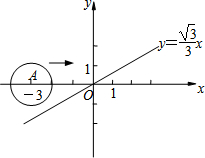 ��ͼ����ƽ��ֱ������ϵ�У�x����һ��A�ӵ㣨-3��0��������x������ƽ�ƣ�����AΪԲ�ģ��뾶Ϊ1��Բ�뺯��y=$\frac{\sqrt{3}}{3}$x��ͼ������ʱ����A�������Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�x����һ��A�ӵ㣨-3��0��������x������ƽ�ƣ�����AΪԲ�ģ��뾶Ϊ1��Բ�뺯��y=$\frac{\sqrt{3}}{3}$x��ͼ������ʱ����A�������Ϊ��������
 ��ͼ����ƽ��ֱ������ϵ�У�x����һ��A�ӵ㣨-3��0��������x������ƽ�ƣ�����AΪԲ�ģ��뾶Ϊ1��Բ�뺯��y=$\frac{\sqrt{3}}{3}$x��ͼ������ʱ����A�������Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�x����һ��A�ӵ㣨-3��0��������x������ƽ�ƣ�����AΪԲ�ģ��뾶Ϊ1��Բ�뺯��y=$\frac{\sqrt{3}}{3}$x��ͼ������ʱ����A�������Ϊ��������| A�� | ��-2��0�� | B�� | ��-$\sqrt{3}$��0����$\sqrt{3}$��0�� | C�� | ��-$\sqrt{3}$��0�� | D�� | ��-2��0����2��0�� |
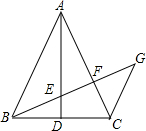 ��ͼ��ʾ���ڡ�ABC�У�AB=AC��AD��BC��CG��AB��BG�ֱ�AD��AC��E��F����$\frac{EF}{BE}=\frac{2}{3}$����ô$\frac{GE}{BE}$��ֵΪ$\frac{3}{2}$��
��ͼ��ʾ���ڡ�ABC�У�AB=AC��AD��BC��CG��AB��BG�ֱ�AD��AC��E��F����$\frac{EF}{BE}=\frac{2}{3}$����ô$\frac{GE}{BE}$��ֵΪ$\frac{3}{2}$�� ��ͼ���ñ߳�Ϊ4��2��������ƴ����ͼ��ʾͼ�Σ���ͼ����Ӱ���ֵ����Ϊ$\frac{8}{3}$��
��ͼ���ñ߳�Ϊ4��2��������ƴ����ͼ��ʾͼ�Σ���ͼ����Ӱ���ֵ����Ϊ$\frac{8}{3}$��