题目内容
18.南京青奥会开幕在即,某服装店老板小陈用3600元购进甲乙两款运动服,很快售完.小陈再次去购进同款、同数量的服装时,他发现甲、乙俩款服装的进价分别上涨了20元/件、5元/件,结果比上次多花了400元.设小陈每次购买甲服装x件,乙服装y件.(1)请直接写出y与x之间的函数关系式:y=-4x+80.
(2)小陈经计算后发现,第二次进货时甲、乙两款服装的平均单价比第一次上涨了8元.
①求x、y的值.
②第二次所购进的服装全部卖出后获利35%,小陈带着这批服装的全部销售款再去进货,这时两款服装均恢复了最初的进价,于是小陈花了3000元购买乙服装,其余钱款全部购买甲服装,结果所购进甲、乙两款服装数量恰好相等.问:这次小陈共购买了多少件服装?
分析 (1)根据甲、乙俩款服装的进价分别上涨了20元/件、5元/件,结果比上次多花了400元,可得20x+5y=400,即y=-4x+80;
(2)根据第二次进货时甲、乙两款服装的平均单价比第一次上涨了8元,得到8(x+y)=400,联立20x+5y=400,得到方程组,即可解答;
(3)先计算出第二次的销售款为5400元,设老板小陈第一次购进甲、乙两款运动服的单价分别为a、b元,根据题意得到方程组$\left\{\begin{array}{l}{10a+40b=3600}\\{\frac{3000}{b}=\frac{5400-3000}{a}}\end{array}\right.$,即可解答.
解答 解:(1)根据题意得:20x+5y=400,即y=-4x+80,
故答案为:y=-4x+80.
(2)①根据题意得:$\left\{\begin{array}{l}{20x+5y=400}\\{8(x+y)=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=40}\end{array}\right.$.
∴小陈每次购买甲服装10件,乙服装40件.
②第二次服装的销售款为:(3600+400)×(1+35%)=5400(元),
设老板小陈第一次购进甲、乙两款运动服的单价分别为a、b元,
根据题意得:
$\left\{\begin{array}{l}{10a+40b=3600}\\{\frac{3000}{b}=\frac{5400-3000}{a}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=60}\\{b=75}\end{array}\right.$,
∴$\frac{3000}{75}$=40,
40×2=80(件),
答:这次小陈共购进80件服装.
点评 本题考查了一次函数的应用,解决本题的关键是应用已知条件得到方程组进行解决问题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 一 二 三 | B. | 二 三 四 | C. | 一 二 四 | D. | 一 三 四 |
| A. | 相切 | B. | 相离 | C. | 相离或相切 | D. | 相切或相交 |
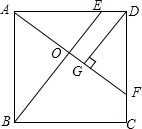 如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G. 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20.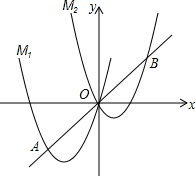 如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.
如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.
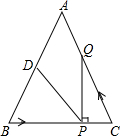 如图,在等腰三角形ABC中,点P、Q分别为线段BC、CA上的动点,点P从点B出发沿BC方向运动,点Q从点C出发沿CA方向运动,两点同时以2cm/s的速度从B、C出发,当P到达C或Q到达A时停止运动,已知D为AB的中点,AB=AC=10cm,BC=8cm,设运动时间为t(s).
如图,在等腰三角形ABC中,点P、Q分别为线段BC、CA上的动点,点P从点B出发沿BC方向运动,点Q从点C出发沿CA方向运动,两点同时以2cm/s的速度从B、C出发,当P到达C或Q到达A时停止运动,已知D为AB的中点,AB=AC=10cm,BC=8cm,设运动时间为t(s).