题目内容
11. 如图,用边长为4和2的正方形拼成如图所示图形,则图中阴影部分的面积为$\frac{8}{3}$.
如图,用边长为4和2的正方形拼成如图所示图形,则图中阴影部分的面积为$\frac{8}{3}$.
分析 首先证得△CEG∽△ADG,得到DG=$\frac{8}{3}$,然后根据阴影部分的面积等于两正方形的面积和-S△ABE-S△ADG即可得解.
解答  解:∵四边形ABCD,CEFG是正方形,
解:∵四边形ABCD,CEFG是正方形,
∴AB=CD,∠ABC=∠BCD=∠GCE=90°,AD∥CE,
∴△CEG∽△ADG,
∴$\frac{CG}{DG}$=$\frac{CE}{AD}$,
∵CE=$\frac{1}{2}$AD,
∴CG=$\frac{1}{2}$DG,
∴DG=$\frac{8}{3}$,
∴S阴影=S正方形ABCD+S正方形CEFG-S△ABE-S△ADG
=4×4+2×2-$\frac{1}{2}×4×6$-$\frac{1}{2}×4×\frac{8}{3}$
=$\frac{8}{3}$.
故答案为$\frac{8}{3}$.
点评 本题考查了正方形的性质,相似三角形的判定和性质,关键是证明△CEG∽△ADG.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
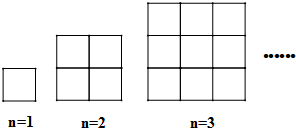
2.如图是用火柴棍摆成的边长分别是1,2,3根火柴棍时的正方形,当边长为10根火柴棍时,摆出的正方形所用的火柴棍的根数为( )

| A. | 220 | B. | 200 | C. | 120 | D. | 100 |
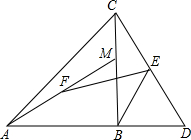 如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )
如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )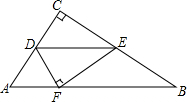 如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( ) 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20.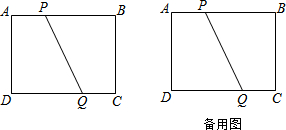
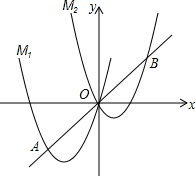 如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.
如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.