题目内容
13．实数tan45°，$\root{3}{8}$，0，-$\frac{3}{5}$π，$\sqrt{9}$，-$\frac{1}{3}$，sin60°，0.3131131113…（相邻两个3之间依次多一个1），其中无理数的个数是（ ）| A． | 4 | B． | 2 | C． | 1 | D． | 3 |
分析 掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，结合题意判断即可．
解答 解：在实数tan45°，$\root{3}{8}$，0，-$\frac{3}{5}$π，$\sqrt{9}$，-$\frac{1}{3}$，sin60°，0.3131131113…（相邻两个3之间依次多一个1）中，
无理数有：-$\frac{3}{5}$π，sin60°，0.3131131113…（相邻两个3之间依次多一个1），共3个，
故选D．
点评 此题主要考查了无理数的定义，熟记无理数的三种形式，①开方开不尽的数，②无限不循环小数，③含有π的数是解题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
3．为了解某校1800名学生的身高情况，从中抽取了200名学生的身高，就这个问题来说，下面结论正确的是（ ）
| A． | 1800名学生是总体 | B． | 1800名学生的身高是总体 | ||
| C． | 200名学生是所抽取的一个样本 | D． | 每个学生是个体 |
如图，AC与BD相交于点O，且AB=CD，请添加一个条件∠A=∠C，使得△ABO≌△CDO．
18．已知边长为m的正方形面积为12，则下列关于m的说法中，错误的是（ ）
①m是无理数；
②m是方程m2-12=0的解；
③m满足不等式组$\left\{\begin{array}{l}{m-4＞0}\\{m-5＜0}\end{array}\right.$；
④m是12的算术平方根．
①m是无理数；
②m是方程m2-12=0的解；
③m满足不等式组$\left\{\begin{array}{l}{m-4＞0}\\{m-5＜0}\end{array}\right.$；
④m是12的算术平方根．
| A． | ①② | B． | ①③ | C． | ③ | D． | ①②④ |
如图，建筑物AB后有一座假山，其坡度为i=1：$\sqrt{3}$，山坡上E点处有一凉亭，测得假山坡脚C与建筑物水平距离BC=25米，与凉亭距离CE=20米，某人从建筑物顶端测得E点的俯角为45°，求建筑物AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）
5．九年级数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤70且x为整数）天的售价目与销量的相关信息如下表：
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于3250元？请直接写出结果．
| 时间x（天） | 1≤x≤40 | 40≤x≤70 |
| 售价（元/件） | x+45 | 85 |
| 每天销售（件） | 150-2x | |
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于3250元？请直接写出结果．
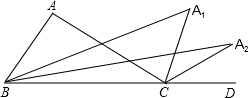如图，在△ABC，∠BAC=100°，延长BC到D，∠ABC与∠ACD的角平分线相交于A1，若∠A1BC与∠A1CD的角平分线相交于点A2，以此类推，∠An-1BC与∠An-1CD的角平分线相交于点An，则∠An=$\frac{100°}{{2}^{n}}$．