��Ŀ����
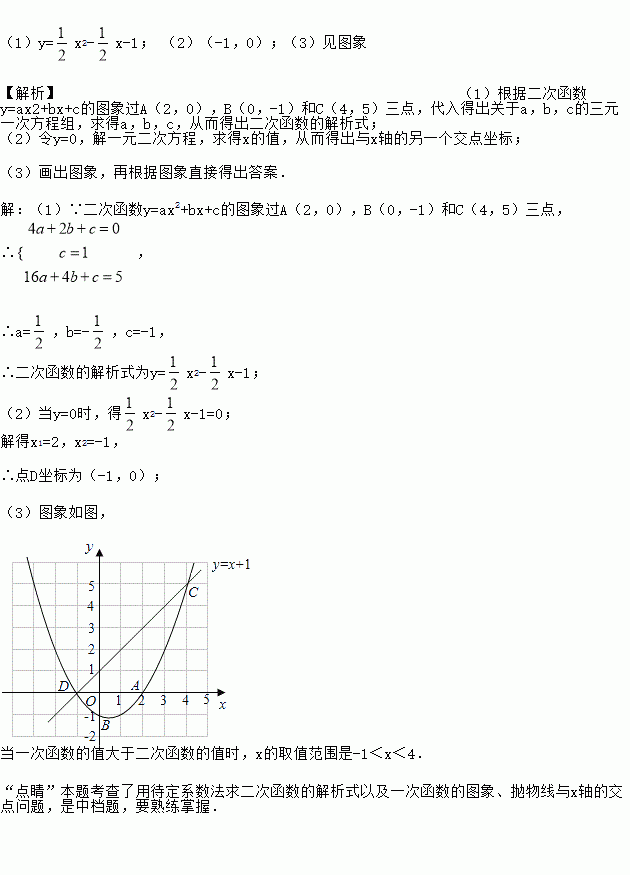
��ͼ����֪���κ���y=ax2+bx+c��ͼ���A(2��0)��B(0��-1)��C(4��5)���㣮
(1)����κ����Ľ���ʽ��
(2)����κ�����ͼ����x�����һ������ΪD�����D�����ꣻ
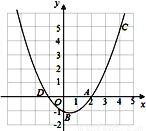
(3)��ͬһ����ϵ�л���ֱ��y=x+1����д����x��ʲô��Χ��ʱ��һ�κ�����ֵ���ڶ��κ�����ֵ��
 ��1��y=x2-x-1�� ��2����-1��0������3����ͼ��
����������1�����ݶ��κ���y=ax2+bx+c��ͼ���A��2��0����B��0��-1����C��4��5�����㣬����ó�����a��b��c����Ԫһ�η����飬���a��b��c���Ӷ��ó����κ����Ľ���ʽ��
��2����y=0����һԪ���η��̣����x��ֵ���Ӷ��ó���x�����һ���������ꣻ
��3������ͼ���ٸ���ͼ��ֱ�ӵó��𰸣�
��������
��1��...
��1��y=x2-x-1�� ��2����-1��0������3����ͼ��
����������1�����ݶ��κ���y=ax2+bx+c��ͼ���A��2��0����B��0��-1����C��4��5�����㣬����ó�����a��b��c����Ԫһ�η����飬���a��b��c���Ӷ��ó����κ����Ľ���ʽ��
��2����y=0����һԪ���η��̣����x��ֵ���Ӷ��ó���x�����һ���������ꣻ
��3������ͼ���ٸ���ͼ��ֱ�ӵó��𰸣�
��������
��1��...
��·��Sһ��ʱ���ٶȦ���ʱ��t֮��ĺ�����ϵ�� ( )
A. ���������� B. ���������� C. һ�κ��� D. ���κ���
 B
�����������������֪v=����·��Sһ������֪�ٶ�v��ʱ��t֮��ĺ�����ϵ�Ƿ���������.
��ѡ��B.
B
�����������������֪v=����·��Sһ������֪�ٶ�v��ʱ��t֮��ĺ�����ϵ�Ƿ���������.
��ѡ��B. ���и�ʽ�����ҵı����У��Ƿֽ���ʽ���� ( )
A. x2-9+6x��(x+3)(x-3)+6x B. (x+5)(x-2)��x2+3x-10
C. x2-8x+16��(x-4)2 D. (x-2)(x+3)��(x+3)(x-2)
 C
����������һ������ʽ���ɼ�����ʽ�Ļ�����ʽ���������������ʽ�ֽ���ʽ.������ʽ�ֽ�Ķ���ɵã�ֻ��ѡ��C������ʽ�ֽ����ʽ����ѡC.
C
����������һ������ʽ���ɼ�����ʽ�Ļ�����ʽ���������������ʽ�ֽ���ʽ.������ʽ�ֽ�Ķ���ɵã�ֻ��ѡ��C������ʽ�ֽ����ʽ����ѡC. ����2��5������4��5����������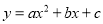 �ϵ������������ĶԳ��ᣨ ��
�ϵ������������ĶԳ��ᣨ ��
A. x=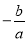 B.
B. 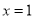 C.
C. 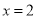 D.
D. 
 D
�������������������Ϊ��(2,5)��(4,5)���������ϣ�
��������������������ȵ����㣬��������ƽ�������ǶԳ��ᣬ
����,�Գ���
��ѡD.
D
�������������������Ϊ��(2,5)��(4,5)���������ϣ�
��������������������ȵ����㣬��������ƽ�������ǶԳ��ᣬ
����,�Գ���
��ѡD. �����ж��κ����У���ͼ��Գ���Ϊx=-2���ǣ�������
A. 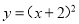
B. 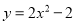
C. 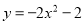
D. 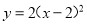
 A
�����������ݶ��κ���������������������ĶԳ��ᣬ�ɵã�
�ĶԳ���Ϊx=-2����A��ȷ��
�ĶԳ���Ϊx=0����B����
�ĶԳ���Ϊx=0����C����
�ĶԳ���Ϊx=2����D����
��ѡ��A��
A
�����������ݶ��κ���������������������ĶԳ��ᣬ�ɵã�
�ĶԳ���Ϊx=-2����A��ȷ��
�ĶԳ���Ϊx=0����B����
�ĶԳ���Ϊx=0����C����
�ĶԳ���Ϊx=2����D����
��ѡ��A�� ������Ķ��κ���ͼ����������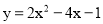 ����ͬ�Ķ��㣬�����ڶԳ������࣬y��x������������ڶԳ�����Ҳ࣬y��x���������С����������κ����Ľ���ʽΪ��������
����ͬ�Ķ��㣬�����ڶԳ������࣬y��x������������ڶԳ�����Ҳ࣬y��x���������С����������κ����Ľ���ʽΪ��������
A. 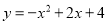
B. 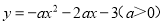
C. 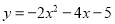
D. 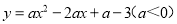
 D
��������������y=2x2-4x-1�Ķ�������Ϊ��1��-3�����������������Ķ��κ����Ľ���ʽ�Ķ��������ǣ�1��-3�����������߿������£�
A�������߿������£����������ǣ�1��5��������ѡ�����
B�������߿������£����������ǣ�1��-3a-3��������ѡ�����
C�������߿������£����������ǣ�-1��-3��������ѡ�����
D�������߿������£����������ǣ�1��-3��...
D
��������������y=2x2-4x-1�Ķ�������Ϊ��1��-3�����������������Ķ��κ����Ľ���ʽ�Ķ��������ǣ�1��-3�����������߿������£�
A�������߿������£����������ǣ�1��5��������ѡ�����
B�������߿������£����������ǣ�1��-3a-3��������ѡ�����
C�������߿������£����������ǣ�-1��-3��������ѡ�����
D�������߿������£����������ǣ�1��-3��... ��֪���κ���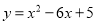 ��
��
��1������ʽ��Ϊ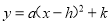 ����ʽ��
����ʽ��
��2������ú���ͼ����x�ᡢy��Ľ������꣮
 ��1����2����1��0������5��0������0��5��
����������������1��ͨ���䷽�õ�����2���Ȱ������ߵĽ���ʽд�ɽ���ʽ�õ�=��x-1����x-5�������ɵõ���������x��Ľ������ꣻ��x=0����ԭ������ϵʽ��ȷ����������y��Ľ������꣮
�����������1����
��2����=��x-1����x-5����
����������x�ύ������Ϊ��1��0������5��0����
��x=0��y=-5��
������...
��1����2����1��0������5��0������0��5��
����������������1��ͨ���䷽�õ�����2���Ȱ������ߵĽ���ʽд�ɽ���ʽ�õ�=��x-1����x-5�������ɵõ���������x��Ľ������ꣻ��x=0����ԭ������ϵʽ��ȷ����������y��Ľ������꣮
�����������1����
��2����=��x-1����x-5����
����������x�ύ������Ϊ��1��0������5��0����
��x=0��y=-5��
������... �����κ���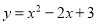 ��Ϊ
��Ϊ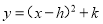 ����ʽ�����Ϊ��������
����ʽ�����Ϊ��������
A. 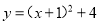
B. 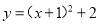
C. 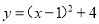
D. 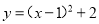
 D
��������
��ѡ��D��
D
��������
��ѡ��D�� ���κ���y=ax2+bx+c����b2=ac����x=0ʱ��y=��4��������
A. y���=��4 B. y��С=��4 C. y���=��3 D. y��С=��3
 C
�������������������x=0��y=-4����ɵã�c=-4�����ݿɵã� ���ʺ��������ֵ�������ֵΪ�� ����ѡC��
C
�������������������x=0��y=-4����ɵã�c=-4�����ݿɵã� ���ʺ��������ֵ�������ֵΪ�� ����ѡC��