题目内容
8.有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形(图③),则图③中的阴影部分的正方形的边长等于m-n(用含m、n的代数式表示)
(2)请用两种不同的方法列代数式表示图③中阴影部分的面积.
方法①(m+n)2-4mn 方法②(m-n)2
(3)请你观察图形③,写出三个代数式(m+n)2、(m-n)2、mn关系的等式:(m-n)2=(m+n)2-4mn;
(4)根据(3)题中的等量关系,解决如下问题:若已知x+y=7,xy=10,则(x-y)2=9;
(5)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞.则(a+2b)2-8ab的值为4cm2.
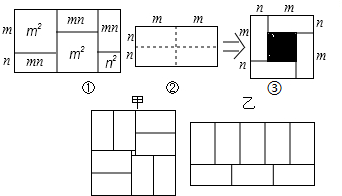
分析 (1)阴影部分的正方形的边长为m-n;
(2)方法①:阴影部分的面积=大正方形的面积-4个小长方形的面积;方法②:表示出小正方形的边长为m-n,即可解答;
(3)大正方形的面积减去4个小长方形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m-n)2、mn之间的等量关系;
(4)根据(3)所得出的关系式,可求出(x-y)2的值;
(5)利用图形面积之间关系得出(a+2b)2-8ab=(a-2b)2即可求出.
解答 解:(1)阴影部分的正方形的边长为m-n;
故答案为:m-n.
(2)方法①:阴影部分的面积=大正方形的面积-4个小长方形的面积,
所以阴影部分的面积为:(m+n)2-4mn;
方法②:表示出小正方形的边长为m-n,
所以阴影部分的面积=(m-n)2.
故答案为:(m+n)2-4mn;(m-n)2.
(3)(m-n)2=(m+n)2-4mn;
故答案为:(m-n)2=(m+n)2-4mn.
(4)(x-y)2=(x+y)2-4xy=72-4×10=9;
故答案为:9.
(5)∵(a+2b)2-8ab=(a-2b)2=22=4(cm2),
∴(a+2b)2-8ab的值为4cm2.
故答案为:4cm2.
点评 本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
18.下列说法中正确的个数是( )
①如果一个事件发生的可能性很小,那么他就不可能发生
②如果一个事件发生的概率很大,那么他就必然发生
③如果一个事件不可能发生,那么其发生的概率为0.
①如果一个事件发生的可能性很小,那么他就不可能发生
②如果一个事件发生的概率很大,那么他就必然发生
③如果一个事件不可能发生,那么其发生的概率为0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
19.对于四边形ABCD,给出下列4组条件:①∠A=∠B=∠C=∠D;②∠B=∠C=∠D;③∠A=∠B,∠C=∠D;④∠A=∠B=∠C=90°,其中能得到“四边形ABCD是矩形”的条件有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
16.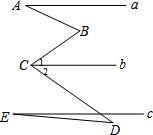 如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )
如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )
 如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )
如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )| A. | 50°,30° | B. | 60°,30° | C. | 50°,20° | D. | 60°,20° |