题目内容
19.关于x的一元二次方程ax2+bx+$\frac{1}{4}$=0有实数根,写出一组满足条件的实数a,b的值:a=1,b=1.分析 根据二次项系数不为0以及根的判别式b2-4ac≥0,即可得出关于a、b的二元二次不等式组,解不等式组得出a、b的关系,随便写一组满足条件的a、b值即可.
解答 解:∵关于x的一元二次方程ax2+bx+$\frac{1}{4}$=0有实数根,
∴有$\left\{\begin{array}{l}{a≠0}\\{{b}^{2}-a≥0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a≠0}\\{{b}^{2}≥a}\end{array}\right.$.
$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$满足该条件.
故答案为:1;1.
点评 本题考查了根的判别式,解题的关键是得出关于a、b的二元二次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据根的个数由根的判别式得出关于系数的不等式(或不等式组)是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k≠0 | D. | k≥-1 |
4.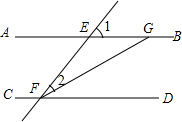 如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
 如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )
如图,AB∥CD,∠1=70°,FG平分∠EFD,则∠2的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 70° |
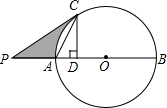 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,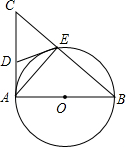 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.