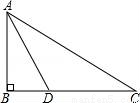
题目内容
6.计算:(1)(2$\sqrt{3}$-5$\sqrt{2}$)($\sqrt{3}-2\sqrt{2}$);
(2)($\frac{\sqrt{3}}{3}$-$\sqrt{2}$)($\frac{\sqrt{2}}{2}$$+\sqrt{3}$);
(3)($\frac{\sqrt{5}+1}{2}$)2+($\frac{\sqrt{5}-1}{2}$)2;
(4)$\frac{\sqrt{5}+1}{2}•\frac{\sqrt{5}-1}{2}$.
分析 (1)利用多项式乘多项式的计算方法计算;
(2)利用多项式乘多项式的计算方法计算;
(3)先利用完全平方公式计算,然后合并同类二次根式;
(4)利用平方差公式计算.
解答 解:
(1)(2$\sqrt{3}$-5$\sqrt{2}$)($\sqrt{3}-2\sqrt{2}$)
=6-4$\sqrt{6}$-5$\sqrt{6}$+20
=26-9$\sqrt{6}$;
(2)($\frac{\sqrt{3}}{3}$-$\sqrt{2}$)($\frac{\sqrt{2}}{2}$$+\sqrt{3}$)
=$\frac{\sqrt{6}}{6}$+1-1-$\sqrt{6}$
=-$\frac{5\sqrt{6}}{6}$;
(3)($\frac{\sqrt{5}+1}{2}$)2+($\frac{\sqrt{5}-1}{2}$)2
=$\frac{6+2\sqrt{5}}{4}$+$\frac{6-2\sqrt{5}}{4}$
=3;
(4)$\frac{\sqrt{5}+1}{2}•\frac{\sqrt{5}-1}{2}$
=$\frac{5-1}{4}$
=1.
点评 此题考查二次根式的混合运算,注意先化简,再进一步利用计算公式和计算方法计算.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
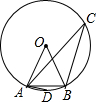 如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
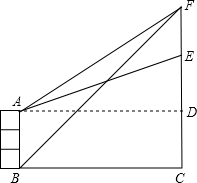 如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$)
如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$)
 和一次函数y=kx+2的图象大致是( )
和一次函数y=kx+2的图象大致是( )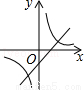 B.
B. 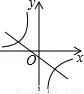
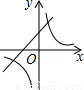 D.
D. 
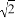 ≈1.414,
≈1.414,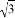 ≈1.732.
≈1.732.