题目内容
8.已知在平行四边形ABCD中,点M、N分别是边AB、BC的中点,如果$\overrightarrow{AB}=\overrightarrow a$、$\overrightarrow{AD}=\overrightarrow b$,那么向量$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$(结果用$\overrightarrow a$、$\overrightarrow b$表示).分析 首先根据题意画出图形,然后连接AC,由三角形法则,即可求得$\overrightarrow{AC}$,然后由点M、N分别是边AB、BC的中点,根据三角形中位线的性质,求得答案.
解答 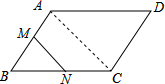 解:如图,连接AC,
解:如图,连接AC,
∵四边形ABCD是平行四边形,
∴$\overrightarrow{BC}$=$\overrightarrow{AD}$=$\overrightarrow{b}$,
∵$\overrightarrow{AB}=\overrightarrow a$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
∵点M、N分别是边AB、BC的中点,
∴$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
故答案为:$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识、平行四边形的性质以及三角形中位线的性质.注意掌握三角形法则的应用是关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
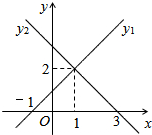 如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.
如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1. 如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.
如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.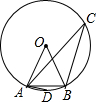 如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
 和一次函数y=kx+2的图象大致是( )
和一次函数y=kx+2的图象大致是( )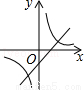 B.
B. 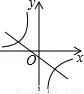
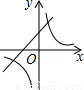 D.
D.