题目内容
10.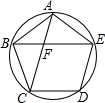 如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.
如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.(1)求证:AB2=AF•AC;
(2)设AF=m,CF=n,求m:n的值.
分析 (1)根据题意得到五边形ABCDE为⊙O的内接正五边形,于是得到∠ABF=∠BAF=∠ACB=36°,∠CBF=∠CFB=72°,推出△ABF∽△ACB,根据相似三角形的性质即可得到结论.
(2)由(1)知AB=CF=n,根据AB2=AF•AC=AF•(AF+CF),代入已知条件解方程组即可得到结论.
解答 (1)证明:A、B、C、D、E是⊙O上的五个等分点,
∴五边形ABCDE为⊙O的内接正五边形,
其每个内角为$\frac{{({5-2})×{{180}°}}}{5}={108°}$,
∴∠ABF=∠BAF=∠ACB=36°,∠CBF=∠CFB=72°,
∴△ABF∽△ACB,AB=BC=CF,
∴$\frac{AB}{AC}=\frac{AF}{AB}$,
∴AB2=AF•AC;
(2)解:由(1)有AB=CF=n,
由AB2=AF•AC=AF•(AF+CF),
∴n2=m(m+n),
∴m2+mn-n2=0,
即($\frac{m}{n}$)2+($\frac{m}{n}$)-1=0,而$\frac{m}{n}$>0,
解得$\frac{m}{n}=\frac{{\sqrt{5}-1}}{2}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理,正五边形的内角和,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.
如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.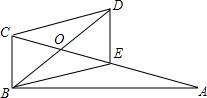 如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.
如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.