题目内容
18.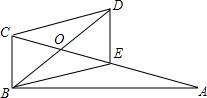 如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.
如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.
分析 延长DE交AB于F,由平行四边形的性质和已知条件得出CB∥DE,CB=DE,∠CBD=∠DBF=∠BDE=45°,得出∠DFB=90°,由直角三角形斜边上的中线性质得出BE=EC=EA,由平行线的性质得出F为AB的中点,由三角形中位线定理得出EF=$\frac{1}{2}$CB,设EF=m,则CB=2m,DE=2m,DF=3m,FB=3m,由勾股定理求出DB,得出DO,CO,即可得出结果.
解答 解:延长DE交AB于F,如图所示: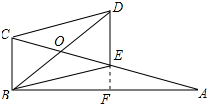
∵∠ABC=90°,四边形ABCD是平行四边形,BD平分∠ABC,
∴CB∥DE,CB=DE,∠CBD=∠DBF=∠BDE=45°,
∴∠DFB=90°,
∵E为AC的中点,
∴BE=EC=EA,
∵EF∥CB,
∴F为AB的中点,
∴EF=$\frac{1}{2}$CB,
设EF=m,则CB=2m,DE=2m,DF=3m,FB=3m,
∴DB=$\sqrt{D{F}^{2}+B{F}^{2}}$=3$\sqrt{2}$m,
∴DO=$\frac{1}{2}$DB=$\frac{3\sqrt{2}}{2}$m,
∴CO=$\frac{1}{2}$CE=$\frac{1}{2}$BE=$\frac{1}{2}$$\sqrt{{m}^{2}+9{m}^{2}}$=$\frac{\sqrt{10}}{2}$m,
∴$\frac{OC}{OD}$=$\frac{\frac{\sqrt{10}}{2}m}{\frac{3\sqrt{2}}{2}m}$=$\frac{\sqrt{5}}{3}$.
点评 本题考查了平行四边形的性质、勾股定理、直角三角形斜边上的中线性质、三角形中位线定理等知识;熟练掌握平行四边形的性质,由勾股定理求出DB是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
8.若4x2-5xy-6y2=0,其中xy≠0,则$\frac{x+y}{x-y}$的值为( )
| A. | -3或$\frac{1}{7}$ | B. | 3或-$\frac{1}{7}$ | C. | 3 | D. | $\frac{1}{7}$ |
6.一件商品的原价是100元,经过两次提价后的价格为123元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 100(1+x)=123 | B. | 100(1-x)=123 | C. | 100(1+x)2=123 | D. | 100(1-x)2=123 |
13.在下列6个图形中,每个小四边形都是全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的编号是( )
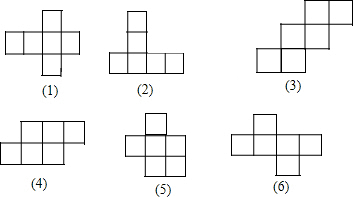

| A. | ①②③④ | B. | ①②⑥ | C. | ①③④ | D. | ①③⑥ |
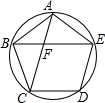 如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.
如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.