题目内容
15.已知x=22,y=-7,则$\frac{1}{x-3y}$$-\frac{6y}{{x}^{2}-9{y}^{2}}$的值为( )| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
分析 先通分,再把分子相加减,把x、y的值代入进行计算即可.
解答 解:原式=$\frac{1}{x-3y}$-$\frac{6y}{(x+3y)(x-3y)}$
=$\frac{x+3y-6y}{(x+3y)(x-3y)}$
=$\frac{x-3y}{(x+3y)(x-3y)}$
=$\frac{1}{x+3y}$,
当x=22,y=-7时,原式=$\frac{1}{22-21}$=1.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
相关题目
6.一件商品的原价是100元,经过两次提价后的价格为123元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
| A. | 100(1+x)=123 | B. | 100(1-x)=123 | C. | 100(1+x)2=123 | D. | 100(1-x)2=123 |
20.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之差的绝对值为2或4的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
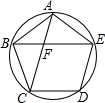 如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.
如图,A、B、C、D、E是⊙O上的五个等分点,连接AC、BE相交于点F.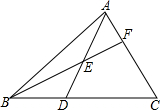 如图,在△ABC中,D为BC边上一点,E为线段AD上一点,延长BE交AC于点F.若$\frac{BD}{BC}=\frac{2}{5}$,$\frac{AE}{AD}=\frac{1}{2}$,则$\frac{AF}{AC}$=$\frac{2}{7}$.
如图,在△ABC中,D为BC边上一点,E为线段AD上一点,延长BE交AC于点F.若$\frac{BD}{BC}=\frac{2}{5}$,$\frac{AE}{AD}=\frac{1}{2}$,则$\frac{AF}{AC}$=$\frac{2}{7}$.