题目内容
 如图:小明在大楼的东侧A处发现仰角为75°的方向上有一热气球,此时小亮在大楼的西侧B处测得气球的仰角为30°.已知AB的距离为120m,设气球所在位置为C,且A、B、C三点在同一平面上,试求此时小明、小亮与气球的距离AC和BC(结果保留根号).
如图:小明在大楼的东侧A处发现仰角为75°的方向上有一热气球,此时小亮在大楼的西侧B处测得气球的仰角为30°.已知AB的距离为120m,设气球所在位置为C,且A、B、C三点在同一平面上,试求此时小明、小亮与气球的距离AC和BC(结果保留根号).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:先根据三角形外角的性质求出∠C度数,再过点A作AD⊥BC于点D,由直角三角形的性质求出AD及BD的长,再由直角三角形的性质求出CD的长,继而求得AC的长.
解答: 解:∵∠CAE是△ABC的外角,
解:∵∠CAE是△ABC的外角,
∴∠C=∠CAE-∠ABC=75°-∠ACB=45°,
过点A作AD⊥BC于点D,
∵AB=120m,
∴AD=
AB=60m;
∴BD=AB•cos30°=120×
=60
(m),
∵△ACD是等腰直角三角形,
∴AD=CD=60m,
∴BC=BD+CD=60
+60(m),AC=
=60
(m).
 解:∵∠CAE是△ABC的外角,
解:∵∠CAE是△ABC的外角,∴∠C=∠CAE-∠ABC=75°-∠ACB=45°,
过点A作AD⊥BC于点D,
∵AB=120m,
∴AD=
| 1 |
| 2 |
∴BD=AB•cos30°=120×
| ||
| 2 |
| 3 |
∵△ACD是等腰直角三角形,
∴AD=CD=60m,
∴BC=BD+CD=60
| 3 |
| AD |
| sin45° |
| 2 |
点评:此题考查了仰角的定义.根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,AD∥BC,∠D=96°,∠A=104°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
如图,AD∥BC,∠D=96°,∠A=104°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.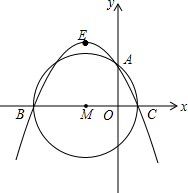 如图,平面直角坐标系中,B(-4,0),C(1,0),以BC为直径作⊙M,交y轴正半轴于点A,过A、B、C三点作抛物线.
如图,平面直角坐标系中,B(-4,0),C(1,0),以BC为直径作⊙M,交y轴正半轴于点A,过A、B、C三点作抛物线. 如图,等边△ABC的边长为7cm,M为△ABC内任意一点,MD∥AC,ME∥AB,MF∥BC,求MD+ME+MF的值.
如图,等边△ABC的边长为7cm,M为△ABC内任意一点,MD∥AC,ME∥AB,MF∥BC,求MD+ME+MF的值.
 如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法: