Question

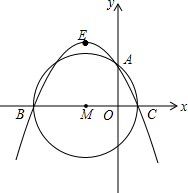如图，平面直角坐标系中，B（-4，0），C（1，0），以BC为直径作⊙M，交y轴正半轴于点A，过A、B、C三点作抛物线．
（1）求点A的坐标；
（2）求抛物线解析式；
（3）P（x，y）为抛物线上一动点，若∠BPC为锐角，写出x的取值范围；
（4）记E为抛物线的顶点，动点F从点E出发，沿线段EM以速度v₁运动到点Q后，再以速度v₂沿直线向点C运动，若v₁：v₂=

41

：4，要使点F从点E到点C的用时最短，试确定点Q的坐标．

Answer 1

考点：二次函数综合题

专题：

分析：（1）A点首先在圆上，同时又在抛物线上，由（2）的目标是求抛物线解析式，所以本问肯定要运用圆的知识，连接AM，△AMO即为直角三角形，且AM，MO长易知，所以AO易知，A坐标易得．
（2）由A，B，C三点坐标已知，则抛物线用待定系数法求解即可，但注意B、C为抛物线与x轴的两个交点，使用y=a（x+4）（x-1）计算较简单．
（3）用时最短在初看本题并不好理解，把问题搞清楚是我们解决问题的第一要务，所以可以任在EM上找一点Q，然后过Q作BE的垂线简单计算了解题目想要真正传达我们的信息．计算三角形EBM时发现其边长中含有

41

，且进一步发现在Rt△EQN中，

EQ

NQ

=

41

4

，即EQ=

41

4

NQ．而v₁=

41

4

v₂，而t=

EQ

v1

+

CQ

v2

=

41 4 NQ

41 4 v2

+

QC

v2

=

NQ+QC

v2

，即当NQ+QC最短时，t最小．此时问题转化为垂线段最短的问题，结论易得．

解答：解：（1）如图1，连接AM．
∵B（-4，0），C（1，0），
∴BC=5，
∴AM=BM=CM=

5

2

，
∴OM=CM-OC=

3

2

，
∴根据勾股定理，AO=

AM2-OM2

=2，
∴A点坐标为（0，2）．

（2）∵抛物线过B（-4，0），C（1，0），
∴设抛物线为y=a（x+4）（x-1），
∴抛物线过A（0，2），
∴将A（0，2）代入y=a（x+4）（x-1），解得a=-

1

2

，
∴抛物线为y=-

1

2

（x+4）（x-1）=-

1

2

x2-

3

2

x+2．

（3）如图2，记抛物线与圆的另一个交点为D，易得D点坐标为（-3，2），
∵当P点在B左边，DA之间，C右边时，∠BPC为锐角，
∴当x＜-4或-3＜x＜0或x＞1时，∠BPC为锐角．

（4）如图3，连接BE，过点Q，作QN⊥BE，
∵抛物线为y=-

1

2

x2-

3

2

x+2，
∴根据二次函数性质可得，顶点E坐标为（-

3

2

，

25

8

）．
∵M（-

3

2

，0），B（-4，0），
∴EM=

25

8

．
在Rt△EBM中，
∵BM=

5

2

，
∴BE=

5

8

41

，
∴sin∠BEM=

BM

BE

=

4

41

，
∴在Rt△EQN中，

EQ

NQ

=

41

4

，即EQ=

41

4

NQ．
∵v₁：v₂=

41

：4
∴v₁=

41

4

v₂，
∴t=

EQ

v1

+

CQ

v2

=

41 4 NQ

41 4 v2

+

QC

v2

=

NQ+QC

v2

，
∴当NQ+QC最短时，t最小．
如图4，记BE与⊙M交点为N，连接CN交EM于点Q，此时NQ+QC最短，此时∠BEM=∠BCN．
∵在Rt△BEM中，tan∠BEM=

BM

EM

=

5 2

25 8

=

4

5

，
∴在Rt△QMC中，QM=MC•tan∠BCN=MC•tan∠BEM=

5

2

•

4

5

=2，
∴Q点坐标为（-

3

2

，2）．

点评：本题主要考察了圆的性质、待定系数法求解二次函数解析式、解直角三角形及利用垂线段最短求解最值等问题．前两问是非常常规的题目，最后一问在初看本题并不好理解，所以要首先任在EM上找一点Q，然后过Q作BE的垂线简单计算以了解题目想要真正传达我们的信息．