题目内容
16.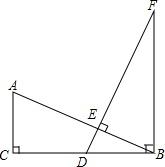 已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.
已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.
分析 根据余角的性质得到∠A=∠BDE,根据全等三角形的判定定理得到△ABC≌△BDF,由全等三角形的性质即可得到结论.
解答 证明:∵∠ACB=∠FBD=∠90°,
∵DE⊥AB,
∴∠A+∠ABC=∠ABC+∠BDE=90°,
∴∠A=∠BDE.
在△ABC与△BDF中,
$\left\{\begin{array}{l}{∠A=∠BDF}\\{AC=BD}\\{∠C=∠DBF=90°}\end{array}\right.$,
∴△ABC≌△BDF,
∴AB=DF.
点评 本题考查了全等三角形的判定和性质,余角的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
6.下列计算正确的是( )
| A. | (x+2)(x-2)=x2-2 | B. | (a+b)(b-a)=a2-b2 | C. | (-a+b)2=a2-2ab+b2 | D. | (-a-b)2=a2-2ab+b2 |
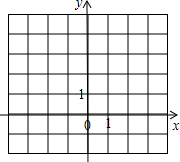 在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).
在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).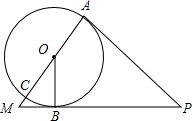 如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.
如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.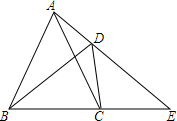 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.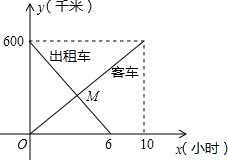 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示. (1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.
(1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.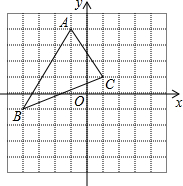 如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)
如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)