题目内容
5.(1)解不等式:$1-\frac{2x+1}{3}≥\frac{1-x}{2}$;(2)用配方法解方程:x2+4x-1=0.
分析 (1)利用①去分母;②去括号;③移项;④合并同类项;⑤化系数为1的步骤解出不等式;
(2)根据完全平方公式和配方法解出方程即可.
解答 解:(1)去分母,得6-2(2x+1)≥3(1-x)
去括号,得6-4x-2≥3-3x
移项,得-4x+3x≥3-6+2
合并同类项,得-x≥-1
系数化为1,得,x≤1;
(2)x2+4x-1=0,
x2+4x+4=1+4,
(x+2)2=5,
x+2=±$\sqrt{5}$,
x1=$\sqrt{5}$-2,x2=$-\sqrt{5}$-2.
点评 本题考查的是一元一次不等式的解法、配方法解一元二次方程,掌握解一元一次不等式的一般步骤、配方法的一般步骤是解题的关键.

练习册系列答案
相关题目
13.坐标平面内有两点P(x,y),Q(m,n),若x+m=0,y-n=0,则点P与点Q( )
| A. | 关于x轴对称 | B. | 无对称关系 | C. | 关于原点对称 | D. | 关于y轴对称 |
15.体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
(1)全班有多少名同学?
(2)组距是多少?组数是多少?
(3)跳绳的次数x在100≤x<140范围内的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息;
(5)你怎样评价这个班的跳绳成绩?
| 次数 | 频数 |
| 60≤x<80 | 2 |
| 80≤x<100 | 4 |
| 100≤x<120 | 21 |
| 120≤x<140 | 13 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 1 |
(2)组距是多少?组数是多少?
(3)跳绳的次数x在100≤x<140范围内的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息;
(5)你怎样评价这个班的跳绳成绩?
 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.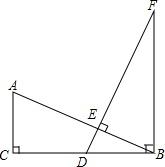 已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.
已知:如图,在△ABC中,∠ACB=90°,点D在BC上,且BD=AC,过点D作DE⊥AB于点E,过点B作CB的垂线,交DE的延长线于点F.求证:AB=DF.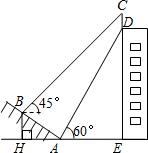 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:$\sqrt{3}$,AB=8米,AE=10米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)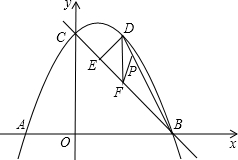 已知:如图,直线y=-x+2与x轴交于B点,与y轴交于C点,A点坐标为(-1,0).
已知:如图,直线y=-x+2与x轴交于B点,与y轴交于C点,A点坐标为(-1,0).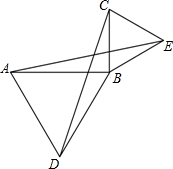 如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.
如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.